
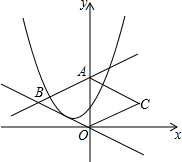
 如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,
如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,分析 (1)通过解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-\frac{1}{2}x}\end{array}\right.$得B(-2,1),由于点C与B点关于y轴对称,则C(2,1);
(2)先求出A(0,2),直线OC的解析式为y=$\frac{1}{2}$x,根据二次函数的性质得抛物线y=(x-m)2+k的顶点坐标为(m,k),把(m,k)代入y=-$\frac{1}{2}$x得k=-$\frac{1}{2}$m,则抛物线解析式为y=(x-m)2-$\frac{1}{2}$m,当抛物线与OC相切时,即抛物线的对称轴右侧与直线相切,M的值最小,则方程(x-m)2-$\frac{1}{2}$m=$\frac{1}{2}$x有相等的实数解,利用判别式的意义可求出m=-$\frac{1}{16}$;当抛物线y=(x-m)2-$\frac{1}{2}$m经过点A(0,2)时,根据二次函数图象上点的坐标特征得m2-$\frac{1}{2}$m=2,解得m1=$\frac{1-\sqrt{33}}{4}$(抛物线对称轴右侧经过点A),m2=$\frac{1+\sqrt{33}}{4}$(抛物线对称轴左侧经过点A),同样当抛物线y=(x-m)2-$\frac{1}{2}$m经过点C(2,1)时,求得m1=$\frac{9-\sqrt{33}}{4}$(抛物线对称轴右侧经过点C),m2=$\frac{9+\sqrt{33}}{4}$(抛物线对称轴左侧经过点C),所以抛物线与△AOC的边OC,AC都有公共点,利用图象可得-$\frac{1}{16}$≤m≤$\frac{9-\sqrt{33}}{4}$或$\frac{1+\sqrt{33}}{4}$≤m≤$\frac{9+\sqrt{33}}{4}$.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-\frac{1}{2}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,
所以B(-2,1);
∵△AOB沿y轴翻折,得到△AOC,
即点C与B点关于y轴对称,
∴C(2,1);
(2)当x=0时,y=$\frac{1}{2}$x+2=2,则A(0,2),
直线OC的解析式为y=$\frac{1}{2}$x,
抛物线y=(x-m)2+k的顶点坐标为(m,k),
把(m,k)代入y=-$\frac{1}{2}$x得k=-$\frac{1}{2}$m,
∴抛物线解析式为y=(x-m)2-$\frac{1}{2}$m,
当抛物线y=(x-m)2-$\frac{1}{2}$m与直线OC相切时,则方程(x-m)2-$\frac{1}{2}$m=$\frac{1}{2}$x有相等的实数解,
整理得x2-(2m+$\frac{1}{2}$)x+m2-$\frac{1}{2}$m=0,则△=(2m+$\frac{1}{2}$)2-4(m2-$\frac{1}{2}$m)=0,解得m=-$\frac{1}{16}$,
当抛物线y=(x-m)2-$\frac{1}{2}$m经过点A(0,2)时,则m2-$\frac{1}{2}$m=2,解得m1=$\frac{1-\sqrt{33}}{4}$,m2=$\frac{1+\sqrt{33}}{4}$,
当抛物线y=(x-m)2-$\frac{1}{2}$m经过点C(2,1)时,则(2-m)2-$\frac{1}{2}$m=1,解得m1=$\frac{9-\sqrt{33}}{4}$,m2=$\frac{9+\sqrt{33}}{4}$,
∵抛物线与△AOC的边OC,AC都有公共点,
∴-$\frac{1}{16}$≤m≤$\frac{9-\sqrt{33}}{4}$或$\frac{1+\sqrt{33}}{4}$≤m≤$\frac{9+\sqrt{33}}{4}$.
故答案为(2,1),-$\frac{1}{16}$≤m≤$\frac{9-\sqrt{33}}{4}$或$\frac{1+\sqrt{33}}{4}$≤m≤$\frac{9+\sqrt{33}}{4}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和关于y轴对称的点的坐标特征;会求直线与直线、抛物线与直线的交点坐标.难点是如何确定抛物线与△AOC的边OC,AC都有公共点时,顶点的位置.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
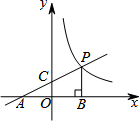 如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.
如图,直线y1=$\frac{1}{2}$x+1分别交x轴,y轴于点A,C,点P是直线AC与双曲线y2=$\frac{k}{x}$(x>0)在第一象限内的交点,PB⊥x轴于点B,△PAB的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 里程 | 甲类收费(元) | 乙类收费(元) |
| 3千米以下(包含3千米) | 5.00 | 6.00 |
| 3千米以上,每增加1千米 | 1.60 | 1.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
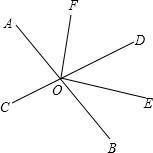 如图,两条直线AB,CD相交于点O,OE平分∠BOD.
如图,两条直线AB,CD相交于点O,OE平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
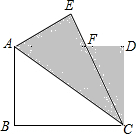 如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.
如图,在矩形ABCD中,AB=6,BC=8,将矩形ABCD沿对角线AC对折,然后放在桌面上,折叠后所成的图形覆盖的面积(阴影部分的面积)是29.25.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).
某学校体育看台的侧面如图中阴影部分所示,看台有四级高度相等的小台阶,已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为0.8米的不锈钢架杆AD和BC(杆子的低端分别为D、C),且∠DAB=66.5°(cos66.5°≈0.4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 10 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com