
| A. | 5 | B. | 10 | C. | $\frac{24}{5}$ | D. | $\frac{12}{5}$ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
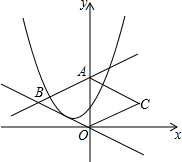 如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,
如图,直线y=$\frac{1}{2}$x+2交y轴于点A,与直线y=-$\frac{1}{2}$x交于点B,把△AOB沿y轴翻折,得到△AOC,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+x>b+x | B. | -a+1<-b+1 | C. | 2a<2b | D. | $\frac{a}{2}$>$\frac{b}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
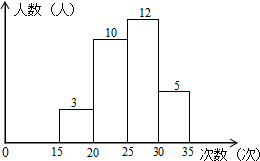 某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1.
某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在15~20之间的频率为0.1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com