
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
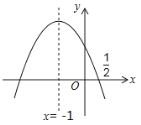
A.①②③B.①③④C.①③④⑤D.②④⑤
【答案】B
【解析】
根据抛物线的开口方向、对称轴、与y轴的交点判定系数符号,及运用一些特殊点解答问题.
由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴左边可得:a,b同号,所以b<0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc>0,故①正确;
直线x=1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以![]() =1,可得b=2a,
=1,可得b=2a,
∵抛物线y=ax2+bx+c的对称轴是x=1.且过点(![]() ,0),
,0),
∴抛物线与x轴的另一个交点坐标为(![]() ,0),
,0),
当x=![]() 时,y=0,当x=
时,y=0,当x=![]() 时,y=0,
时,y=0,
即a×(![]() )2+ b×
)2+ b×![]() +c=0,a×(
+c=0,a×(![]() )2+ b×(
)2+ b×(![]() )+c=0,
)+c=0,
整理得:a+2b+4c=0,25a10b+4c=0,故②错误,③正确;
∵b=2a,当x=-1时,y>0
∴a-b+c>0,a=![]() b
b
∴a-b+c=![]() b-b+c=c-
b-b+c=c-![]() b>0
b>0
故2c-b>0
又b<0,-b>0
∴2c-3b=2c-b-2b>0,故④正确;
∵x=1时,函数值最大,
∴ab+c≥m2amb+c,
∴ab≥m(amb),
当x=-1时,ab=m(amb)所以⑤错误;
故选:B.


科目:初中数学 来源: 题型:
【题目】孙老师在上《等可能事件的概率》这节课时,给同学们提出了一个问题:“如果同时随机投掷两枚质地均匀的骰子,它们朝上一面的点数和是多少的可能性最大?”同学们展开讨论,各抒己见,其中小芳和小超两位同学给出了两种不同的回答.小芳认为6的可能性最大,小超认为7的可能性最大.你认为他们俩的回答正确吗?请用列表或画树状图等方法加以说明.(骰子:六个面上分别刻有1,2,3,4,5,6个小圆点的小正方体.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() ,点
,点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 以每秒
以每秒![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 以每秒2的速度沿折线
以每秒2的速度沿折线![]() 向终点
向终点![]() 运动,设
运动,设![]() 运动的时间为
运动的时间为![]() ,
,![]() ,
,![]() 经过的路线与
经过的路线与![]() 围成的图形面积为
围成的图形面积为![]() ,则
,则![]() 关于
关于![]() 的图象大致是( )
的图象大致是( )
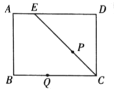
A.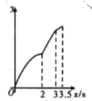 B.
B.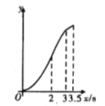 C.
C. D.
D.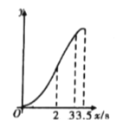
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
![]() 纸是我们学习工作最常用的纸张之一, 其长宽之比是
纸是我们学习工作最常用的纸张之一, 其长宽之比是![]() ,我们定义:长宽之比是
,我们定义:长宽之比是![]() 的矩形纸片称为“标准纸”.
的矩形纸片称为“标准纸”.
操作判断:
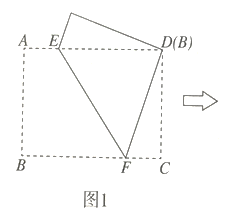
![]() 如图1所示,矩形纸片
如图1所示,矩形纸片![]() 是一张“标准纸”,将纸片折叠一次,使点
是一张“标准纸”,将纸片折叠一次,使点![]() 与
与![]() 重合,再展开,折痕
重合,再展开,折痕![]() 交
交![]() 边于点
边于点![]() 交
交![]() 边于点
边于点![]() ,若
,若![]() 求
求![]() 的长,
的长,
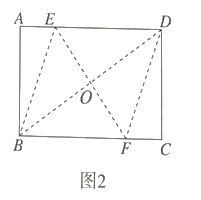
![]() 如图2,在
如图2,在![]() 的基础上,连接
的基础上,连接![]() 折痕
折痕![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 判断四边形
判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
探究发现:
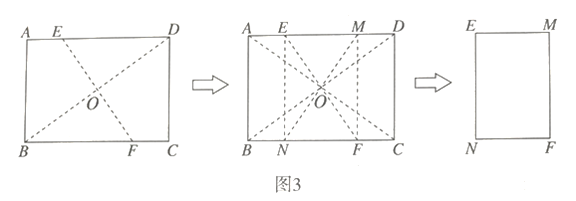
![]() 如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点
如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点![]() 与点
与点![]() 重合,再展开,痕
重合,再展开,痕![]() 交
交![]() 边于点
边于点![]() ,
,![]() 交边于点
交边于点![]() 交
交![]() 也是点
也是点![]() .然后将四边形
.然后将四边形![]() 剪下,探究纸片
剪下,探究纸片![]() 是否为“标准纸”,说明理由.
是否为“标准纸”,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1和图2,矩形ABCD中,E是AD的中点,P是BC上一点,AF∥PD,∠FPE=∠DPE.
(1)作射线PE交直线AF于点G,如图1.
①求证:AG=DP;
②若点F在AD下方,AF=2,PF=7,求DP的长.
(2)若点F在AD上方,如图2,直接写出PD,AF,PF的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月,某大型商业集团随机抽取所属的部分商业连锁店进行评估,将抽取的格商业连锁店按照评估成绩分成了A、B、C、D四个等级,并绘制了如图不完整的扇形统计图和条形统计图.
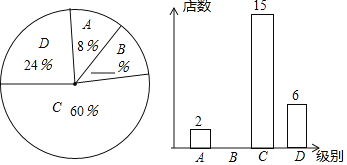
根据以上信息,解答下列问题:
(1)本次评估随机抽取了 家商业连锁店;
(2)请补充完整扇形统计图和条形统计图,并在图中标注相应数据;
(3)从A、B两个等级的商业连锁店中任选2家介绍营销经验,请用列表或画树状图的方法求其中至少有一家是A等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式维的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
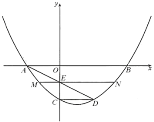
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在抛物线上,且
在抛物线上,且![]() .
.![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 的直线
的直线![]() 平行于
平行于![]() 轴,与抛物线相交于
轴,与抛物线相交于![]() ,
,![]() 两点,则线段
两点,则线段![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com