
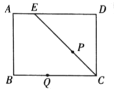
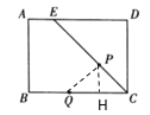
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 上一点,且
上一点,且![]() ,
,![]() ,点
,点![]() ,
,![]() 同时从
同时从![]() 点出发,点
点出发,点![]() 以每秒
以每秒![]() 的速度沿
的速度沿![]() 向终点
向终点![]() 运动,点
运动,点![]() 以每秒2的速度沿折线
以每秒2的速度沿折线![]() 向终点
向终点![]() 运动,设
运动,设![]() 运动的时间为
运动的时间为![]() ,
,![]() ,
,![]() 经过的路线与
经过的路线与![]() 围成的图形面积为
围成的图形面积为![]() ,则
,则![]() 关于
关于![]() 的图象大致是( )
的图象大致是( )
A.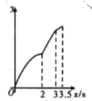 B.
B.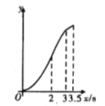 C.
C. D.
D.
【答案】B
【解析】
根据矩形的性质动点BC=AD=4,AB=CD=3,∠BCD=∠D=90°,AD∥BC,求出∠BCE=∠DEC=45°,由勾股定理求出CE=![]() ,分三段:当
,分三段:当![]() 时,当
时,当![]() 时,当
时,当![]() 时,分别求出函数解析式即可进行判断.
时,分别求出函数解析式即可进行判断.
∵四边形ABCD是矩形,
∴BC=AD=4,AB=CD=3,∠BCD=∠D=90°,AD∥BC,
∵![]() ,
,
∴∠BCE=∠DEC=45°,
∴CE=![]() ,
,
当![]() 时,CP=
时,CP=![]() ,CQ=2x,∴PH=CH=x,
,CQ=2x,∴PH=CH=x,
∴![]() ;
;
当![]() 时,CP=
时,CP=![]() ,BQ=2x-4,
,BQ=2x-4,
过点P作PH⊥BC于H,作MN∥AD,则四边形ADNM是矩形,四边形PHCN是矩形,
∴MN=AD=4,PN=CH=x,
∴MP=4-x,
∴![]()
![]()
![]()
=![]() ;
;
当![]() 时,点P与点E重合,
时,点P与点E重合,
∴![]()
![]()
![]() =x+6;
=x+6;
故选:B.



 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线![]() 经过点A(3,0)和点B(0,2).
经过点A(3,0)和点B(0,2).
(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与函数
与函数![]() 的图象交于点C(C在第二象限),若ΔCOB的面积与ΔAOB的面积相等,求出m的值.
的图象交于点C(C在第二象限),若ΔCOB的面积与ΔAOB的面积相等,求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在歌唱比赛中,一位歌手分别转动如下的两个转盘(每个转盘都被分成3等份)一次,根据指针指向的歌曲名演唱两首曲目.
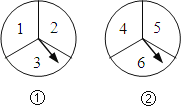
(1)转动转盘①时,该转盘指针指向歌曲“3”的概率是 ;
(2)若允许该歌手替换他最不擅长的歌曲“3”,即指针指向歌曲“3”时,该歌手就选择自己最擅长的歌曲“1”, 请用树形图或列表法中的一种,求他演唱歌曲“1”和“4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.

(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
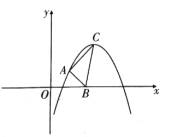
【题目】如图,二次函数![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)已知![]() 点为抛物线上异于
点为抛物线上异于![]() 的一点,且
的一点,且![]() 点横、纵坐标相等,
点横、纵坐标相等,![]() 为
为![]() 轴上任意一点,当
轴上任意一点,当![]() 取最小值时,求出
取最小值时,求出![]() 点坐标和此时
点坐标和此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 内接于
内接于![]() ,
,![]() ,连接
,连接![]() ;
;
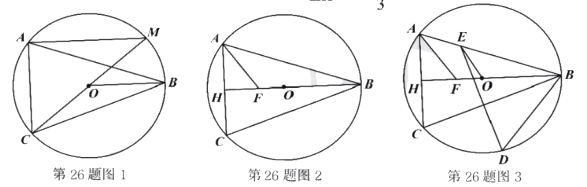
(1)如图1,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(2)如图2,延长![]() 交
交![]() 于点H,点F为BH上一点,连接AF,若
于点H,点F为BH上一点,连接AF,若![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,如图3,点E为AB上一点,点D为![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,若
,若![]() ,
,![]() ,
,![]() ,连接
,连接![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④2c-3b>0;⑤a﹣b≥m(am﹣b)(m≠-1);其中所有正确的结论是( )
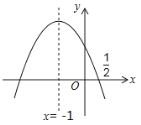
A.①②③B.①③④C.①③④⑤D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
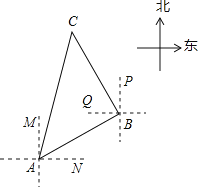
【题目】如图,一艘船由A港沿北偏东60°方向航行20km至B港,然后再沿北偏西30°方向航行20km至C港.
(1)求A,C两港之间的距离;(结果保留到0.1km)
(2)确定C港在A港的什么方向(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com