
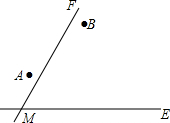
 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部分析 (1)运用尺规作图即可得出结果;
(2)作CD⊥MN于点D.由三角函数得出MD=$\sqrt{3}$CD,DN=$\frac{CD}{tan45°}$=CD,由已知条件得出$\sqrt{3}$CD+CD=2($\sqrt{3}$+1),解得CD=2km即可.
解答 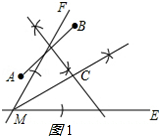 解:(1)答图如图1所示:
解:(1)答图如图1所示:
点C即为所求;
(2)作CD⊥MN于点D.如图2所示:
∵在Rt△CMD中,∠CMN=30°,
∴$\frac{CD}{MD}$=tan∠CMN,
∴MD=$\frac{CD}{tan30°}$=$\frac{CD}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$CD,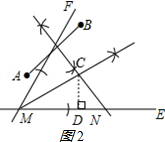 ∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∵在Rt△CND中,∠CNM=45°,$\frac{CD}{DN}$=tan∠CNM,
∴DN=$\frac{CD}{tan45°}$=CD,∵MN=2($\sqrt{3}$+1)km,
∴MN=MD+DN=$\sqrt{3}$CD+CD=2($\sqrt{3}$+1)km.
解得:CD=2km.
答:点C到公路ME的距离为2km.
点评 本题考查了解直角三角形的应用、作图-设计;熟练掌握基本作图和解直角三角形是解决问题的关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不赔不赚 | B. | 赚了8元 | C. | 赚了10元 | D. | 赚了32元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;
如图,在直角坐标系中,一条抛物线与x轴交于A、B两点,与y轴交于C点,其中B(3,0),C(0,4),点A在x轴的负半轴上,OC=4OA;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=__m.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com