
����Ŀ��ij����������һ���н���Ϸ���������£���5��ֽ�ƣ����涼��ϲ����ͷ��������2����Ц��������3���ǿ������ֽ�5��ֽ��ϴ�Ⱥ��泯�ϰڷŵ����ϣ���������ֽ������Ц�����н���û��Ц����û�н���
��1��С�����һ�η��ƻ��ᣬ�������������һ��ֽ�ƣ�С���ý��ĸ����ǣ�
��2��С��������η��ƻ��ᣬ��ͬʱ��������ֽ�ƣ�С����Ϊ�����ý��ĸ�����С��������������ͬ���Ĺ۵�����������ͼ���б������з���˵����
���𰸡�
��1���⣺ ![]() ������0.4��
������0.4��
��2���⣺����ͬ���Ĺ۵㣮
�� ![]() ��
�� ![]() �ֱ��������Ц����
�ֱ��������Ц���� ![]() ��
�� ![]() ��
�� ![]() �ֱ�������ſ��������������б����£�
�ֱ�������ſ��������������б����£�
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
��Ҳ�ɻ�����ͼ��ʾ���ɱ�����Կ��������ܵĽ����20�֣����еý��Ľ����14�֣����С���ý��ĸ��� ![]() ��Ϊ
��Ϊ ![]() ��
�� ![]() ������С���ý��ĸ��ʲ���С����������
������С���ý��ĸ��ʲ���С����������
�����������ø��ʹ�ʽ�������ע�Ľ����������ȵĽ��������������ɣ���2��ʱ���Ϊ�������裬��һ����5���������2����4���������20���������ע�Ľ����14�֣�������С��������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��L1��y=k1x+b1 �� L2��y=k2x+b2 �� ��L1��L2 �� ����k1k2=��1��
��1��Ӧ�ã���֪y=2x+1��y=kx��1��ֱ����k��
��2��ֱ�߾���A��2��3��������y= ![]() x+3��ֱ�������ʽ��
x+3��ֱ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
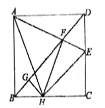
����Ŀ����ͼ����������![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ���㣬
��һ���㣬![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ������
������![]() ���������ĸ������У���
���������ĸ������У���![]() ����
����![]() ����
����![]() ����
����![]() ���ܳ�Ϊ12��������ȷ�Ľ�����__________������ţ�
���ܳ�Ϊ12��������ȷ�Ľ�����__________������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
��������һ����λ��������n�����n�ĸ�����λ�ϵ����ֻ�����ͬ���Ҷ���Ϊ�㣬��ô�������Ϊ��İ����������һ����İ��������������λ�ϵ����ֽ���˳���Եõ�5����ͬ������İ������������6��İ�����ĺ���111���̼�ΪM(n).����n=123�����Եõ�132.213.231.312.321��5���µ���İ����������6����İ�������ĺ�Ϊ123��132��213��231��312��321=1332����Ϊ![]() ������M(123)=12.
������M(123)=12.
(1)���㣺M(125)��M(361)��ֵ��
(2)��s��t������İ������������4��2�ֱ���s��ʮλ��λ�ϵ����֣�2��5�ֱ���t�İ�λ��λ�ϵ����֣���t��ʮλ�ϵ����ֱ�s�İ�λ�ϵ�����С2���涨��![]() .��
.��![]() ����k��ֵ�Ƕ��٣�
����k��ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ǡ�ABC�У���BAC��60��BD��CEΪ�ߣ�FΪBC���е㣬����DE��DF��EF������ۣ���DF��EF����AD��AB��AE��AC���ۡ�DEF�ǵȱ������Σ���BE��CD��BC���ݵ���ABC��45ʱ��BE��![]() DE�У�һ����ȷ���� ��
DE�У�һ����ȷ���� �� 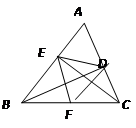
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���ABCD��![]() �ᣬ��
�ᣬ��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ���ı���ABCD���ϵ�һ�����㣮
���ı���ABCD���ϵ�һ�����㣮
��1�����ı���ABCD�����Σ����![]() �����꣮
�����꣮
��2����ͼ1����![]() ����
����![]() �ڵ���������
�ڵ���������
������![]() �ڱ�
�ڱ�![]() ��
��![]() �ϣ���
�ϣ���![]() ����������ԳƵĵ�
����������ԳƵĵ�![]() ����ֱ��
����ֱ��![]() �ϣ����
�ϣ����![]() �����꣮
�����꣮
������![]() �ڱ�
�ڱ�![]() ��
��![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ��Ľ��㣬��ͼ2������
��Ľ��㣬��ͼ2������![]() ��
��![]() ���ƽ����
���ƽ����![]() ������
������![]() ��
��![]() ���ƽ����
���ƽ����![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ۣ�����
���ۣ�����![]() �Ķ�Ӧ��������������ʱ�����
�Ķ�Ӧ��������������ʱ�����![]() �����꣮��ֱ��д���𰸣�
�����꣮��ֱ��д���𰸣�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
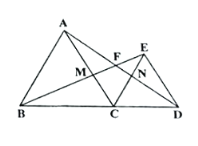
����Ŀ����ͼ����֪��C���߶�BD��һ�㣬��BC�� DCΪһ����BD��ͬһ�����ȱߡ�ABC�͵ȱߡ�ECD,����AD, BE�ཻ�ڵ�F, AC��BE���ڵ�M, AD, CE���ڵ�N,(ע���ȱ������ε�ÿһ���ڽǶ�����60�� )
(1) ��֤�� AD=BE
(2) �߶�CM��CN�����?��֤����Ľ��ۡ�
(3) ���BFD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���![]() �У�
��![]() ����
����![]() �ֱ�ӵ�
�ֱ�ӵ�![]() ͬʱ��������
ͬʱ��������![]() ��
��![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶�����
�˶�����![]() ��
��![]() ���ٶ��ɵ�
���ٶ��ɵ�![]() ���
���![]() �˶����˶�ʱ��Ϊ
�˶����˶�ʱ��Ϊ![]() ����
����![]() __________��ʱ��
__________��ʱ��![]() Ϊƽ���ı��ε�һ�ߣ�
Ϊƽ���ı��ε�һ�ߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
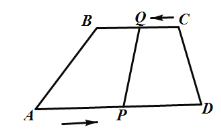
����Ŀ����ͼ���ı���ABCD�У�AB��CD��AB��BC��AB��BC��AB��CD��AE��BD��E��BC��F.

(1)��AB��2CD��
����֤��BC��2BF��
����CE����DE��6��CE��![]() ����EF�ij���
����EF�ij���
(2)��AB��6����CE����СֵΪ______.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com