
【题目】如图,![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() ,当点
,当点![]() 、
、![]() 、
、![]() 三点共线时,旋转角为
三点共线时,旋转角为![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,下面结论:①
,下面结论:①![]() 为等腰三角形;②
为等腰三角形;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 中,正确结论的个数是( )
中,正确结论的个数是( )
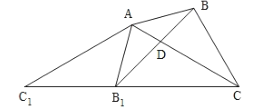
A.2个B.3个C.4个D.5个
【答案】C
【解析】
首先根据旋转性质得出![]() ,从而对结论①进行判断,然后通过对三角形内部角度之间的计算进一步对结论④进行判断,再后通过证明∠
,从而对结论①进行判断,然后通过对三角形内部角度之间的计算进一步对结论④进行判断,再后通过证明∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD对结论②进行判断,再者进一步求出∠
=∠BCD对结论②进行判断,再者进一步求出∠![]() 的度数,由此判断结论③,最后过点D作DM⊥
的度数,由此判断结论③,最后过点D作DM⊥![]() ,通过证明△ABD~△
,通过证明△ABD~△![]() ,利用相似三角形性质进一步分析结论⑤,据此即可得出答案.
,利用相似三角形性质进一步分析结论⑤,据此即可得出答案.
由旋转性质可知:![]() ,
,
∴![]() 为等腰三角形,即①正确;
为等腰三角形,即①正确;
∵∠ACB=30°,
∴∠![]() =∠
=∠![]() =30°,
=30°,
又∵∠![]() =∠BAC=45°,
=∠BAC=45°,
∴∠![]() =75°,
=75°,
∴∠![]() =180°75°30°=75°,
=180°75°30°=75°,
∴CA=![]() ,即④正确;
,即④正确;
∵∠BAC=45°,
∴∠![]() =45°+75°=120°,
=45°+75°=120°,
∵![]() =AB,
=AB,
∴∠![]() =∠ABD=30°,
=∠ABD=30°,
在△![]() 与△BCD中,
与△BCD中,
∵∠![]() =∠BDC,∠
=∠BDC,∠![]() =∠BCD=30°,
=∠BCD=30°,
∴△![]() ~△BCD,即②正确;
~△BCD,即②正确;
∵∠![]() =∠
=∠![]() +∠
+∠![]() =120°,
=120°,
∴旋转角![]() ,即③错误;
,即③错误;
在△ABD与△![]() 中,
中,
∵∠ABD=∠![]() ,∠ADB=∠
,∠ADB=∠![]() ,
,
∴△ABD~△![]() ,
,
∴![]() ,
,
如图,过点D作DM⊥![]() ,
,
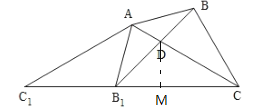
设DM=![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴AC=![]() ,
,
∴AD=![]() ,
,
∴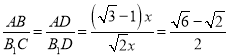 ,即⑤正确;
,即⑤正确;
综上所述,共4个正确,
故选:C.


科目:初中数学 来源: 题型:
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校根据学校实际,决定开设![]() :篮球、
:篮球、![]() :乒乓球、
:乒乓球、![]() :声乐、
:声乐、![]() :健美操四种活动项目(必选且只能选一个),为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果整理后会制成如图所示的不完整的统计图.请你根据图中提供的信息回答下列问题:
:健美操四种活动项目(必选且只能选一个),为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果整理后会制成如图所示的不完整的统计图.请你根据图中提供的信息回答下列问题:
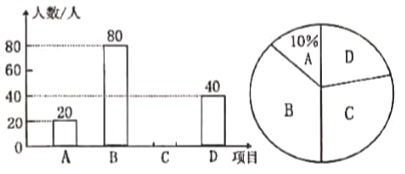
(1)求这次被调查的学生共有多少人;
(2)通过计算补全条形统计图;
(3)已知该校有学生1600人,请根据调查结果估计该校最喜欢乒乓球的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
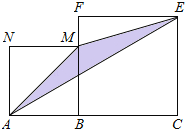
【题目】如图,线段AC=n+1(其中n为正整数),点B在线段AC上,在线段AC同侧作正方形ABMN及正方形BCEF,连接AM、ME、EA得到△AME.当AB=1时,△AME的面积记为S1;当AB=2时,△AME的面积记为S2;当AB=3时,△AME的面积记为
S3;则S3﹣S2= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新建成学校举行美化绿化校园活动,九年级计划购买![]() ,
,![]() 两种花木共100棵绿化操场,其中
两种花木共100棵绿化操场,其中![]() 花木每棵50元,
花木每棵50元,![]() 花木每棵100元.
花木每棵100元.
(1)若购进![]() ,
,![]() 两种花木刚好用去8000元,则购买了
两种花木刚好用去8000元,则购买了![]() 两种花木各多少棵?
两种花木各多少棵?
(2)如果购买![]() 花木的数量不少于
花木的数量不少于![]() 花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
花木的数量,请设计一种购买方案使所需总费用最低,并求出该购买方案所需总费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,对于直线![]() 同侧的
同侧的![]() 、
、![]() 两点,若在
两点,若在![]() 上的点
上的点![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,
上的反射点,![]() 与
与![]() 的和称为
的和称为![]() 、
、![]() 两点的反射距离.
两点的反射距离.

(1)如图2,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 、
、![]() 两点在直线
两点在直线![]() 上的反射点,求
上的反射点,求![]() 、
、![]() 两点的反射距离;
两点的反射距离;
(2)如图3,![]() 内接于
内接于![]() ,直径
,直径![]() 为4,
为4,![]() ,点
,点![]() 为劣弧
为劣弧![]() 上一动点,点
上一动点,点![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,当
上的反射点,当![]() 、
、![]() 两点的反射距离最大时,求劣弧
两点的反射距离最大时,求劣弧![]() 的长;
的长;
(3)如图4,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点,同时点
上的反射点,同时点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点.
上的反射点.
①请判断线段![]() 和
和![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
②求![]() 、
、![]() 两点的反射距离与
两点的反射距离与![]() 、
、![]() 两点的反射距离的比值.
两点的反射距离的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C均在坐标轴上,AO=BO=CO=1,过A,O,C作⊙D,E是⊙D上任意一点,连结CE, BE,则![]() 的最大值是( )
的最大值是( )

A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
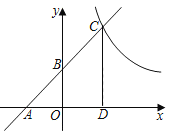
【题目】如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点A、B两点,且与反比例函数y=![]() 的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.
的图象在第一象限内的部分交于点C,CD垂直于x轴于点D,其中OA=OB=OD=2.
(1)直接写出点A、C的坐标;
(2)求这两个函数的表达式;
(3)若点P在y轴上,且S△ACP=14,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com