练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．已知x=$\frac{\sqrt{8}-\sqrt{7}}{\sqrt{8}+\sqrt{7}}$，y=$\frac{\sqrt{8}+\sqrt{7}}{\sqrt{8}-\sqrt{7}}$，求$\frac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}$的值．

    分析 化简x、y的值，代入化简后的代数式即可求得．

    解答 解：∵x=$\frac{\sqrt{8}-\sqrt{7}}{\sqrt{8}+\sqrt{7}}$，y=$\frac{\sqrt{8}+\sqrt{7}}{\sqrt{8}-\sqrt{7}}$，
    化简得x=（$\sqrt{8}$-$\sqrt{7}$）2，y=（$\sqrt{8}$+$\sqrt{7}$）2，
    ∵$\frac{x+y+2\sqrt{xy}}{\sqrt{x}+\sqrt{y}}$=$\frac{（\sqrt{x}+\sqrt{y}）^{2}}{\sqrt{x}+\sqrt{y}}$=$\sqrt{x}$+$\sqrt{y}$，
    ∴原式=$\sqrt{8}$-$\sqrt{7}$+$\sqrt{8}$+$\sqrt{7}$=4$\sqrt{2}$．

    点评 本题考查了二次根式的化简，利用平方差公式化简是去掉分母中的根号的方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    12．已知正六边形的外接圆半径是2，则这个正六边形的边长是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．木工师傅用两颗水泥钉就能将一根木条固定在墙壁上，这样做的数学依据是两点确定一条直线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．一斜面的坡度i=1：0.75，一物体由斜面底部沿斜面向前推进了20米，那么这个物体升高了16米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

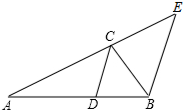    17．如图，已知△ABC的角平分线CD交AB于D点，过点B作BE∥CD交AC的延长线于点E．
    （1）求证：△BCE是等腰三角形；
    （2）若AD=$\sqrt{3}$，BD=$\sqrt{2}$，求$\frac{AC}{CB}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）（-1）2013-|-2|+（$\sqrt{3}-π$）0×$\root{3}{8}$-（$\frac{1}{4}$）-1．
    （2）|-2|+（3-π）0-2-1+$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．对于一元二次方程ax2+bx+c=0（a≠0），有下列四种条件：①b2-4ac＞0；②b2+4ac＞0（a≠0）③a、c异号；④a+b+c的值为零．满足其中之一的方程一定有实数根的有（　　）
    A．1种B．2种C．3种D．4种

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年河南省七年级下学期第一次月考（3月）数学试卷（解析版） 题型：判断题

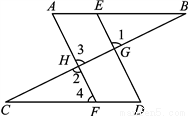
    阅读下面解答过程，填空或填理由．

    已知如图，点E，F分别是AB和CD上的点，DE，AF分别交BC于点G，H，∠A＝∠D，∠1＝∠2.试说明：∠B＝∠C.

    【解析】
    ∵∠1＝∠2 ( )，

    ∠2＝∠3 ( )，

    ∴∠3＝∠1 ( )．

    ∴AF∥DE ( )．

    ∴∠4＝∠D ( )．

    又∵∠A＝∠D ( ），

    ∴∠A＝∠4 ( )．

    ∴AB∥CD ( )．

    ∴∠B＝∠C ( )．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年江苏省七年级下学期第一次月考数学试卷（解析版） 题型：单选题

    如图，已知AB∥CD，则∠A、∠E、∠D之间的数量关系为（　　）

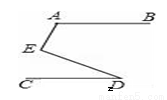
    A. ∠A+∠E+∠D=360° B. ∠A+∠E+∠D=180° C. ∠A+∠E﹣∠D=180° D. ∠A﹣∠E﹣∠D=90°

    查看答案和解析>>

    同步练习册答案