
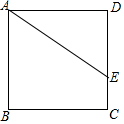
 如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10.
如图,正方形ABCD中,点E在DC边上,DE=4,EC=2,把线段AE绕点A旋转,使点E落在直线BC上的点F处,则FC的长为2或10. 分析 分两种情况进行讨论,①当线段AE顺时针旋转时,利用题干条件得到△ADE≌△ABF1,进而得到FC=EC;②当线段AE逆时针旋转时,利用题干条件得到△ABF2≌△ADE,进而得到F2C=F2B+BC.
解答 解: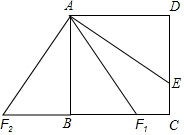
①当线段AD顺时针旋转得到F1点,
在△ADE和△ABF1中,$\left\{\begin{array}{l}{AE=A{F}_{1}}\\{∠D=∠ABC=90°}\\{AD=AB}\end{array}\right.$,
∴△ADE≌△ABF1,
∴DE=BF1=4,
∴EC=F1C=2;
②逆时针旋转得到F2点,同理可得△ABF2≌△ADE,
∴F2B=DE=4,
F2C=F2B+BC=10,
故答案为2或10.
点评 本题主要考查旋转的性质和正方形的性质,解答本题的关键是注意旋转的方向.


科目:初中数学 来源: 题型:解答题
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -$\frac{7}{2}$ | 0 | $\frac{5}{2}$ | 4 | $\frac{9}{2}$ | 4 | m | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
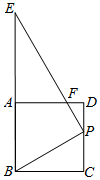 如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.
如图,将一个Rt△BPE与正方形ABCD 叠放在一起,并使其直角顶点P落在线段CD上(不与C,D两点重合),斜边的一部分与线段AB重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
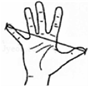 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:
如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.根据最近人体构造学的研究成果表明,一般情况下人的指距d和身高h成某种关系.如表是测得的指距与身高的一组数据:| 指距d(cm) | 20 | 21 | 22 | 23 |
| 身高h(cm) | 160 | 169 | 178 | 187 |
| A. | 25.3厘米 | B. | 26.3厘米 | C. | 27.3厘米 | D. | 28.3厘米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com