
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
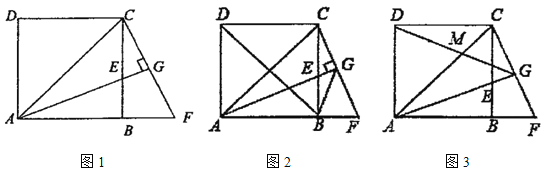
(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() 、
、![]() ,求证
,求证![]() 平分
平分![]() ;
;
(3)如图![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() , 求
, 求![]() 的值。
的值。
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)由正方形性质得出![]() ,
,![]() ,根据直角三角形两锐角互余的关系可得
,根据直角三角形两锐角互余的关系可得![]() ,利用
,利用![]() 可证得
可证得![]() ;
;
(2)由正方形性质与角平分线的定义得出![]() ,利用
,利用![]() 可证得
可证得![]() 得出
得出![]() ,由直角三角形斜边中线的性质得出
,由直角三角形斜边中线的性质得出![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ,即可得出结论;
,即可得出结论;
(3)连接![]() ,由正方形的性质得出
,由正方形的性质得出![]() ,
,![]() ,
,![]() ,推出
,推出![]() ,根据角的和差关系可得
,根据角的和差关系可得![]() ,利用
,利用![]() 可证得
可证得![]() ,得出
,得出![]() ,推出
,推出![]() ,即可证得△DCM∽△ACE,即可得出结果.
,即可证得△DCM∽△ACE,即可得出结果.
(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
(2)证明:∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,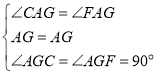 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() 平分
平分![]() .
.
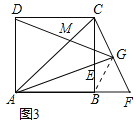
(3)解:连接![]() ,如图3所示:
,如图3所示:
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,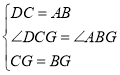 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() =22.5°,
=22.5°,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的网格中建立如图所示的平面直角坐标系,![]() 是格点三角形(顶点是网格线的交点).
是格点三角形(顶点是网格线的交点).
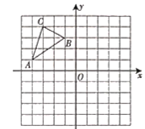
(1)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)画出![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到的
得到的![]() ;
;
(3)在(2)的条件下,![]() 点所经过的路径长为 (结果保留
点所经过的路径长为 (结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,E为AB的中点,将△ADE沿直线DE折叠后,点A落在点F处,DF交对角线AC于G,则FG的长是________.
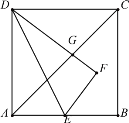
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列是关于四个图案的描述.
图1所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图2所示是一个正三角形内接于圆;
图3所示是一个正方形内接于圆;
图4所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
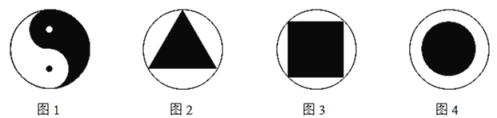
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是( )
A.图1和图3B.图2和图3C.图2和图4D.图1和图4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为以AB为直径的⊙O上一点,AD和过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
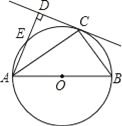
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成![]() 题.
题.
数学课上,老师出示了这样一道题:
如图1,在![]() 中,
中,![]() 点
点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() .点
.点![]() 在
在![]() 延长线上,连接
延长线上,连接![]() .探究线段
.探究线段![]() 与
与![]() 的数量关系并证明.
的数量关系并证明.
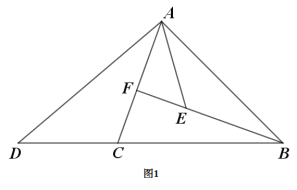
同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小亮:“通过观察和度量,发现![]() 与
与![]() 也相等.”
也相等.”
小伟:“通过边角关系构造辅助线,经过进一步推理, 可以得到线段![]() 与
与![]() 的数量关系.”
的数量关系.”
老师:“保留原题条件,延长图1中的![]() 与
与![]() 相交于点
相交于点![]() (如图2),若知道
(如图2),若知道![]() 与
与![]() 的数量关系,可以求出
的数量关系,可以求出![]() 的值.”
的值.”
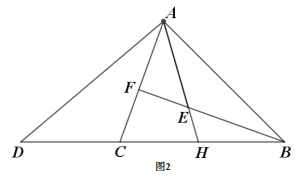
(1)求证:![]() ;
;
(2)求![]() 的值(用含
的值(用含![]() 的式子表示);
的式子表示);
(3)如图2,若![]() 则
则![]() 的值为 (用含
的值为 (用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
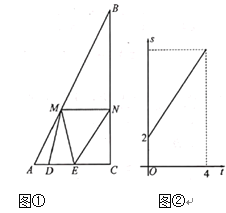
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量![]() (件
(件![]() 与销售价
与销售价![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润W(元![]() 与销售价
与销售价![]() (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
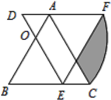
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com