
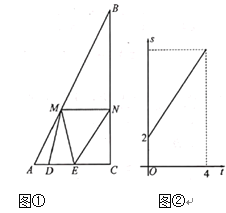
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(1)6,12;(2)![]() 时,
时,![]() 有最大值16.(3)
有最大值16.(3)![]() 或
或![]()
【解析】
(1)当t=4时,点E与C重合,此时AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
由图分析当t=0时,S![]() =2.设M到AC的距离为h,所以
=2.设M到AC的距离为h,所以![]() DE
DE![]() h=2,所以h=2.易求得tan∠A=2,再在Rt
h=2,所以h=2.易求得tan∠A=2,再在Rt![]() 中,解直角三角形可以求出AC的长.
中,解直角三角形可以求出AC的长.
(2) 四边形![]() 的面积等于三角形MDE和三角形MNE的和,用含有t的式子表示出四边形MDEN的面积,再求最值;
的面积等于三角形MDE和三角形MNE的和,用含有t的式子表示出四边形MDEN的面积,再求最值;
(3)两个三角形中已有![]() ,如若再找到一对角相等,两三角形相似,故需分情况进行讨论:当
,如若再找到一对角相等,两三角形相似,故需分情况进行讨论:当![]() 或
或![]() 时,两三角形相似.
时,两三角形相似.
解:(1)由图可知:当t=4时,点E与C重合,此时AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
当t=0时,S![]() =2.设M到AC的距离为h,所以
=2.设M到AC的距离为h,所以![]() DE
DE![]() h=2,所以h=2.
h=2,所以h=2.
∴tan∠A=![]() =2.
=2.
在Rt![]() 中,tan∠A=
中,tan∠A=![]() =2.
=2.
∴BC=2AC=12.
(2)作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]()
![]() ,
,
根据题意,![]() ,
,
∴![]() 时,
时,![]() 有最大值16.
有最大值16.
(3)假设存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
∵![]() ,∴
,∴![]() .
.
①当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
②当![]() 时,
时,![]() ,此时
,此时![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() (舍去)
(舍去)
∴![]() 或
或![]() 时,以
时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.


科目:初中数学 来源: 题型:
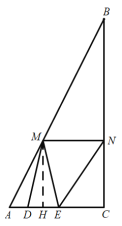
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,延长CE,BA交于点F,连接AC,DF.
(1)求证:四边形ACDF是平行四边形;
(2)当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
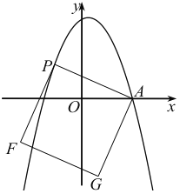
【题目】如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
(1)求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() 、
、![]() ,求证
,求证![]() 平分
平分![]() ;
;
(3)如图![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() , 求
, 求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在![]() 处测得灯塔
处测得灯塔![]() 在船的南偏东60°方向,轮船继续向正东航行30海里后到达
在船的南偏东60°方向,轮船继续向正东航行30海里后到达![]() 处,这时测得灯塔
处,这时测得灯塔![]() 在船的南偏西75°方向,则灯塔
在船的南偏西75°方向,则灯塔![]() 离观测点
离观测点![]() 、
、![]() 的距离分别是( )
的距离分别是( )
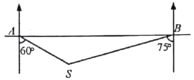
A.![]() 海里、15海里B.
海里、15海里B.![]() 海里、15海里
海里、15海里
C.![]() 海里、
海里、![]() 海里D.
海里D.![]() 海里、
海里、![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
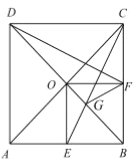
【题目】如图,在边长为1的正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() ,得到以下四个结论:①
,得到以下四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中正确的结论是________(填写序号).
,其中正确的结论是________(填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
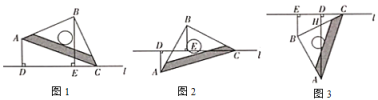
【题目】综合与实践:
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
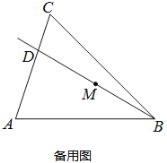
【题目】如图,在△ABC中,![]() ,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
,tanA=3,∠ABC=45°,射线BD从与射线BA重合的位置开始,绕点B按顺时针方向旋转,与射线BC重合时就停止旋转,射线BD与线段AC相交于点D,点M是线段BD的中点.
(1)求线段BC的长;
(2)①当点D与点A、点C不重合时,过点D作DE⊥AB于点E,DF⊥BC于点F,连接ME,MF,在射线BD旋转的过程中,∠EMF的大小是否发生变化?若不变,求∠EMF的度数;若变化,请说明理由.
②在①的条件下,连接EF,直接写出△EFM面积的最小值______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com