
| A. | ①② | B. | ①③ | C. | ③ | D. | ①②④ |
分析 ①根据边长为m的正方形面积为12,可得m2=12,所以m=2$\sqrt{3}$,然后根据$\sqrt{3}$是一个无理数,可得m是无理数,据此判断即可.
②根据m2=12,可得m是方程m2-12=0的解,据此判断即可.
③首先求出不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$的解集是4<m<5,然后根据m=2$\sqrt{3}$<2×2=4,可得m不满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$,据此判断即可.
④根据m2=12,而且m>0,可得m是12的算术平方根,据此判断即可.
解答 解:∵边长为m的正方形面积为12,
∴m2=12,
∴m=2$\sqrt{3}$,
∵$\sqrt{3}$是一个无理数,
∴m是无理数,
∴结论①正确;
∵m2=12,
∴m是方程m2-12=0的解,
∴结论②正确;
∵不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$的解集是4<m<5,m=2$\sqrt{3}$<2×2=4,
∴m不满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$,
∴结论③不正确;
∵m2=12,而且m>0,
∴m是12的算术平方根,
∴结论④正确.
综上,可得
关于m的说法中,错误的是③.
故选:C.
点评 (1)此题主要考查了算术平方根的性质和应用,要熟练掌握,解答此题的关键是要明确:①被开方数a是非负数;②算术平方根a本身是非负数.(3)求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.
(2)此题还考查了无理数和有理数的特征和区别,要熟练掌握,解答此题的关键是要明确:有理数能写成有限小数和无限循环小数,而无理数只能写成无限不循环小数.
(3)此题还考查了不等式的解集的求法,以及正方形的面积的求法,要熟练掌握.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原价 | 每个房间增加10元 | 每个房间增加20元 | … | 每个房间增加10x元 | |
| 每个房价定价 | 180 | 190 | 200 | … | |
| 房住房间数量 | 50 | 49 | 48 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
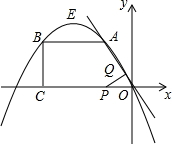 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com