
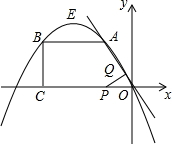
 ��֪����ͼ�����ı���OABC�У�AB��OC��BC��x���ڵ�C��A��-1��1����B��-3��1������P�ӵ�O����������x�Ḻ������ÿ��2����λ���ȵ��ٶ��ƶ�������P��PQ��ֱ��ֱ��OA������Ϊ��Q�����P�ƶ���ʱ��t�루0��t��2��
��֪����ͼ�����ı���OABC�У�AB��OC��BC��x���ڵ�C��A��-1��1����B��-3��1������P�ӵ�O����������x�Ḻ������ÿ��2����λ���ȵ��ٶ��ƶ�������P��PQ��ֱ��ֱ��OA������Ϊ��Q�����P�ƶ���ʱ��t�루0��t��2������ ��1���������߽���ʽΪy=ax2+bx��a��0����Ȼ��ѵ�A��B������������a��b��ֵ�����ɵý⣬�ٰѺ�������ʽ�����ɶ���ʽ��ʽ��Ȼ��д������M�����ꣻ
��2�����ݵ�P���ٶ����OP�����ɵõ���P�����꣬�ٸ��ݵ�A�����������AOC=45�㣬Ȼ���жϳ���POQ�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����������Q�����꼴�ɣ�
��3��������ת�����������O��Q�����꣬Ȼ��ֱ���������߽���ʽ����⼴�ɣ�
��� �⣺��1���������߽���ʽΪy=ax2+bx��a��0����
�ѵ�A��-1��1����B��-3��1������ã�
$\left\{\begin{array}{l}{a-b=1}\\{9a-3b=1}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$��
�������߽���ʽΪy=-$\frac{1}{3}$x2-$\frac{4}{3}$x��
��y=-$\frac{1}{3}$x2-$\frac{4}{3}$x=-$\frac{1}{3}$��x+2��2+$\frac{4}{3}$��
�ඥ��M������Ϊ��-2��$\frac{4}{3}$����
��2���ߵ�P�ӵ�O�����ٶ���ÿ��2����λ���ȣ�
��OP=2t��
���P��������-2t��0����
��A��-1��1����
���AOC=45�㣬
���Q��x�ᡢy��ľ��붼��$\frac{1}{2}$OP=$\frac{1}{2}$����-2t��=-t��
���Q��������t��-t����
��3���ߡ�OPQ���ŵ�P����ʱ�뷽����ת90�㣬
����ת���O��Q�Ķ�Ӧ�������ֱ�Ϊ��2t��-2t������3t��-t����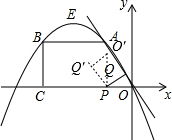
������O���������ϣ���-$\frac{1}{3}$����2t��2-$\frac{4}{3}$����2t��=-2t��
���t=$\frac{1}{2}$��t=0��ȥ����
��t=-$\frac{1}{2}$ʱ����O��-1��1����������y=-$\frac{1}{3}$x2-$\frac{4}{3}$x��
������Q���������ϣ���-$\frac{1}{3}$����3t��2-$\frac{4}{3}$����3t��=-t��
���t=-1��t=0��ȥ����
��t=-1ʱ����Q��-3��1����������y=-$\frac{1}{3}$x2-$\frac{4}{3}$x�ϣ�
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ������ֱ�������ε����ʣ����κ���ͼ���ϵ�����������������ε����������Ĺؼ����ܹ���ͼ�κ͵�������л��Ľ���������ѶȽϴ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ʱ�� | �������� | �������� | |
| A�� | B�� | ||
| ��һ�� | 3̨ | 5̨ | 1800Ԫ |
| �ڶ��� | 4̨ | 10̨ | 3000Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
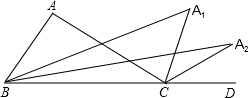 ��ͼ���ڡ�ABC����BAC=100�㣬�ӳ�BC��D����ABC���ACD�Ľ�ƽ�����ཻ��A1������A1BC���A1CD�Ľ�ƽ�����ཻ�ڵ�A2���Դ����ƣ���An-1BC���An-1CD�Ľ�ƽ�����ཻ�ڵ�An�����An=$\frac{100��}{{2}^{n}}$��
��ͼ���ڡ�ABC����BAC=100�㣬�ӳ�BC��D����ABC���ACD�Ľ�ƽ�����ཻ��A1������A1BC���A1CD�Ľ�ƽ�����ཻ�ڵ�A2���Դ����ƣ���An-1BC���An-1CD�Ľ�ƽ�����ཻ�ڵ�An�����An=$\frac{100��}{{2}^{n}}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
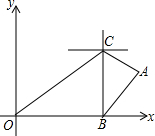 �й���Dz���Һ��ബ���Ϻ������й������ܷ��ɱ����ַ������״���ʾͼ�ϣ����������Һ��ബ������ΪO��0��0����B��80��0����C��80��60��������λ��������Һ��ബ��װ����ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩��
�й���Dz���Һ��ബ���Ϻ������й������ܷ��ɱ����ַ������״���ʾͼ�ϣ����������Һ��ബ������ΪO��0��0����B��80��0����C��80��60��������λ��������Һ��ബ��װ����ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
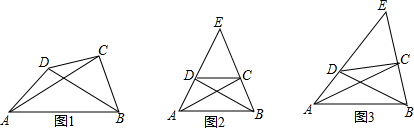
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10��3 | B�� | 10��11 | C�� | 2��3 | D�� | 2��11 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com