
����Ŀ����2019��10��1�յĽ���70��������ϣ��ж���쵼�˳�ϯ�ۿ����ҹ�ʢ����ı���ʽ.Ϊ��ʾ�Ѻã��ҹ�����ѡ������մ������Ʒ��Ϊ�����������е�����.�ף������������ֱ�н�������![]() ��
��![]() ���ִ�����
���ִ�����![]() ���մɵ�����.��������100�������������壬ÿ��ֻ����������һ�ִ��壬�ҹ�������50����������
���մɵ�����.��������100�������������壬ÿ��ֻ����������һ�ִ��壬�ҹ�������50����������![]() ���մ�.
���մ�.![]() ���˾�����������
���˾�����������![]() ���˾�����������3����
���˾�����������3����![]() ���˾���������
���˾���������![]() ���˾���������20%.���������͵Ĺ���
���˾���������20%.���������͵Ĺ���![]() ��
��![]() ��
��![]() ������Ʒ�����˾�����������
������Ʒ�����˾�����������![]() ���˾�����������30%����
���˾�����������30%����![]() ���˾���������Ϊż�����������͵Ĺ���������_________��.
���˾���������Ϊż�����������͵Ĺ���������_________��.
���𰸡�945
��������
��׳�����![]() ����������
����������![]() �ִ��壬
�ִ��壬![]() �ִ�����˾���������Ϊ
�ִ�����˾���������Ϊ![]() �������ݱ������͵Ĺ���
�������ݱ������͵Ĺ���![]() ��
��![]() ��
��![]() ������Ʒ�����˾�����������
������Ʒ�����˾�����������![]() ���˾�����������30%�з�����⼴��.
���˾�����������30%�з�����⼴��.
�⣺��׳�����![]() ����������
����������![]() �ִ��壬
�ִ��壬![]() ����������
����������![]() �ִ��壬
�ִ��壬![]() �ִ�����˾���������Ϊ
�ִ�����˾���������Ϊ![]() ������
������![]() �ִ�����˾���������Ϊ
�ִ�����˾���������Ϊ![]() ����
����![]() ���մɵ��˾���������Ϊ
���մɵ��˾���������Ϊ![]() ����
����
�����⣺![]() .
.
�����ã�![]() ��
��
��![]() ����
����![]() ������
������
��![]() ��
��
��![]() ��
��![]() Ϊż��
Ϊż��
�൱![]() ʱ��
ʱ��![]() ��
��
�ʱ������͵Ĺ��������ļ�Ϊ��![]() ��.
��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
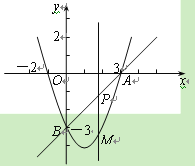
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��x2��mx��n������A(3��0)��
B(0����3)����P��ֱ��AB�ϵĶ��㣬����P��x��Ĵ������������ڵ�M�����P�ĺ�
����Ϊt��
(1)�ֱ����ֱ��AB�����������ߵĽ���ʽ��
(2)����P�ڵ������ޣ�����AM��BM�����߶�PM�ʱ������ABM�������
(3)�Ƿ���������ĵ�P��ʹ���Ե�P��M��B��OΪ������ı���Ϊƽ���ı��Σ������ڣ���ֱ��д����P�ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ʵ��ķ��������з��̣�
��1����x��3��2��24
��2��x2+12x+27��0
��3��x2+6x��4
��4��2��x��3��2��3��x��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1��A��P��B��C�ǡ�O�ϵ��ĸ��㣮��APC=��CPB=60����
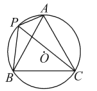
��1���ж���ABC����״�� ��
��2����̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
��3������Pλ��![]() ��ʲôλ��ʱ���ı���APBC�������������������
��ʲôλ��ʱ���ı���APBC�������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BC�ǰ��O��ֱ������P�ǰ�Բ�����е㣬��A�ǻ�BP���е㣬AD��BC��D������AB��PB��AC��BP�ֱ���AD��AC�ཻ�ڵ�E��F��
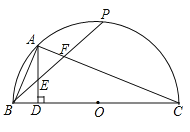
��1����֤��AE=BE��
��2���ж�BE��EF�Ƿ�����𣬲�˵�����ɣ�
��3��С��ͨ����������CF=2AB������С��ķ����Ƿ���ȷ������ȷ����˵�����ɣ�������ȷ����д��CF��AB��ȷ�Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ����֪ʶ�У����̡�����������ʽ�����Ž��ܵ���ϵ�����Ķ�����������ϣ��ش����⣺
���ú���ͼ���ҷ���![]() ��ķ�Χ.�躯��
��ķ�Χ.�躯��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() .����
.����![]() ��ͼ��������
��ͼ��������![]() ��
��![]() ������
������![]() ��
��![]() ���·�����
���·�����![]() ��
��![]() ���Ϸ�����ú���ͼ����
���Ϸ�����ú���ͼ����![]() �ύ�������ش���-2��С��-1.�ʣ�����
�ύ�������ش���-2��С��-1.�ʣ�����![]() ���н⣬�Ҹý�ķ�ΧΪ
���н⣬�Ҹý�ķ�ΧΪ![]() .
.
���϶���
��һԪ���β���ʽ![]() .�������������ˣ����Ϊ���ɵã�
.�������������ˣ����Ϊ���ɵã�
�����![]() ����
����![]() ����
����![]()
�����![]() ����
����![]() ������
������
�ʣ�![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() .
.
��1������ݲ���һ������⣺��֪����![]() ��Ψһ��
��Ψһ��![]() ����
����![]() ��
��![]() ��������������
Ϊ��������������![]() ��ֵ.
��ֵ.
��2�����ϲ���һ����϶�������⣺������![]() �ķ���
�ķ���![]() �Ľ�ֱ�Ϊ
�Ľ�ֱ�Ϊ![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
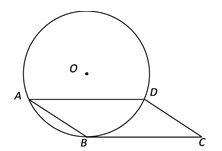
����Ŀ����ͼ������ABCD�У�AD�ǡ�O���ң�BC�ǡ�O�����ߣ��е�ΪB��
��1����֤��![]() ��
��
��2����AB��5��AD��8�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��֪��F��2![]() ��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30����
��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30����
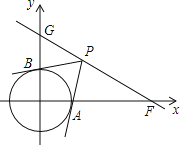
��1��ֱ��д����G�����ꣻ
��2������O�İ뾶Ϊ1����P��ֱ��GF�ϵĶ��㣬ֱ��PA��PB�ֱ�Լ��O�����ڵ�A��B��
�������߳�PB����Сֵ��
���ʣ���ֱ��GF���ǹ����ڵ�P��ʹ�á�APB=60���������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0����y�ύ�ڵ�C����x�ύ��A��B���㣬���е�B������ΪB��4��0���������ߵĶԳ��ύx���ڵ�D��CE��AB�����������ߵĶԳ��ύ�ڵ�E���������н��ۣ���a��0����b��0����4a+2b+c��0����AD+CE��4������������ȷ���۵�����ǡ�_____________________ ����
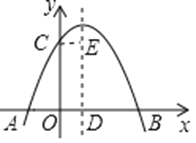
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com