
【题目】如图,在□ABCD中,AD是⊙O的弦,BC是⊙O的切线,切点为B.
(1)求证:![]() ;
;
(2)若AB=5,AD=8,求⊙O的半径.
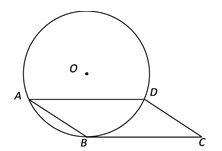
【答案】(1)证明见解析;(2)⊙O的半径为![]()
【解析】
(1) 连接OB,根据题意求证OB⊥AD,利用垂径定理求证;
(2) 根据垂径定理和勾股定理求解.
解:(1)
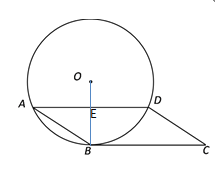
连接OB,交AD于点E.
∵BC是⊙O的切线,切点为B,
∴OB⊥BC.
∴∠OBC=90°
∵ 四边形ABCD是平行四边形
∴AD// BC
∴∠OED=∠OBC =90°
∴ OE⊥AD
又 ∵ OE过圆心O
∴ ![]()
(2)∵ OE⊥AD ,OE过圆心O
∴ AE=![]() AD=4
AD=4
在Rt△ABE中,∠AEB=90°,
BE=![]() =3,
=3,
设⊙O的半径为r,则OE=r-3
在Rt△ABE中,∠OEA=90°,
OE2+AE2 = OA2
即(r-3)2+42= r2 ∴r=![]()
∴⊙O的半径为![]()


科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释效过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
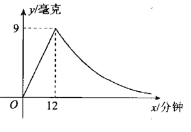
(1)写出从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小区为了促进生活垃圾的分类处理,将生活垃圾分为厨余、可回收和其他三类,分别记为a,b,c,并且设置了相应的垃圾箱,“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱,分别记为A,B,C.
(1)若小明将一袋分好类的生活垃圾随机投入一类垃圾箱,请画树状图或列表求垃圾投放正确的概率;
(2)为调查居民生活垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总共100吨生活垃圾,数据统计如下表(单位:吨):
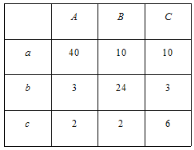
试估计该小区居民“厨余垃圾”投放正确的概率约是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2019年10月1日的建国70周年庆典上,有多国领导人出席观看了我国盛大的阅兵仪式.为表示友好,我国政府选择将刺绣和陶瓷两类工艺品作为国礼赠送给所有的来宾.甲,乙两个工厂分别承接了制作![]() ,
,![]() 两种刺绣与
两种刺绣与![]() 种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作
种陶瓷的任务.甲工厂安排100名工人制作刺绣,每人只能制作其中一种刺绣,乙工厂安排50名工人制作![]() 种陶瓷.
种陶瓷.![]() 的人均制作数量比
的人均制作数量比![]() 的人均制作数量少3件,
的人均制作数量少3件,![]() 的人均制作量比
的人均制作量比![]() 的人均制作量少20%.若本次赠送的国礼(
的人均制作量少20%.若本次赠送的国礼(![]() ,
,![]() ,
,![]() 三样礼品)的人均制作数量比
三样礼品)的人均制作数量比![]() 的人均制作数量少30%,且
的人均制作数量少30%,且![]() 的人均制作数量为偶数件,则本次赠送的国礼共制作了_________件.
的人均制作数量为偶数件,则本次赠送的国礼共制作了_________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 抛物线的顶点.
抛物线的顶点.
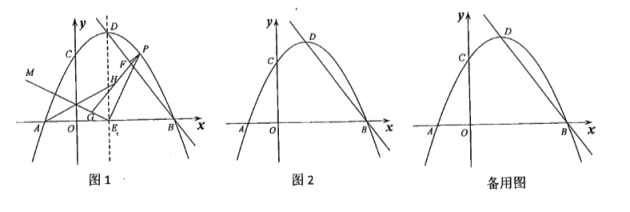
(1)求直线![]() 的解析式;
的解析式;
(2)抛物线对称轴交![]() 轴于点
轴于点![]() ,
,![]() 为直线
为直线![]() 上方的抛物线上一动点,过点
上方的抛物线上一动点,过点![]() 作
作![]() 于点
于点![]() ,当线段
,当线段![]() 的长最大时,连接
的长最大时,连接![]() ,过点
,过点![]() 作射线
作射线![]() ,且
,且![]() ,点
,点![]() 为射线
为射线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),连接
重合),连接![]() ,
,![]() 为
为![]() 中点,连接
中点,连接![]() ,求
,求![]() 的最小值;
的最小值;
(3)如图2,平移抛物线,使抛物线的顶点![]() 在射线
在射线![]() 上移动,点
上移动,点![]() ,
,![]() 平移后的对应点分别为点
平移后的对应点分别为点![]() ,
,![]() ,
,![]() 轴上有一动点
轴上有一动点![]() ,连接
,连接![]() ,
,![]() ,
,![]() 是否能为等腰直角三角形?若能,请求出所有符合条件的
是否能为等腰直角三角形?若能,请求出所有符合条件的![]() 点的坐标;若不能,请说明理由.
点的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(已有经验)
我们已经研究过作一个圆经过两个已知点,也研究过作一个圆与已知角的两条边都相切,尺规作图如图所示:
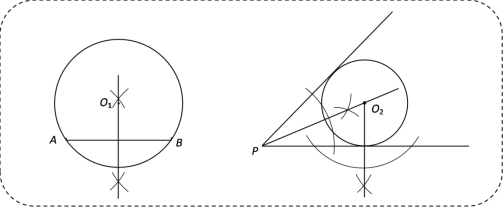
(迁移经验)
(1)如图①,已知点M和直线l,用两种不同的方法完成尺规作图:求作⊙O,使⊙O过M点,且与直线l相切.(每种方法作出一个圆即可,保留作图痕迹,不写作法)

(问题解决)
如图②,在Rt△ABC中,∠C=90°,AC=8,BC=6.
(2)已知⊙O经过点C,且与直线AB相切.若圆心O在△ABC的内部,则⊙O半径r的取值范围为 .
(3)点D是边AB上一点,BD=m,请直接写出边AC上使得∠BED为直角时点E的个数及相应的m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(2)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
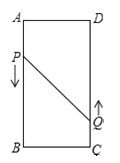
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,△ABC和△A'B'C'的顶点都在边长为1的小正方形的格点上.

(1)填空:∠BAC= °,AB= ;
(2)判断:△ABC和△A'B'C这两个三角形相似吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com