
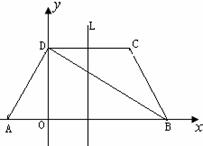
如图所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为![]() 轴,过D且垂直于AB的直线为
轴,过D且垂直于AB的直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(1)求∠DAB的度数及A、D、C三点的坐标;
(2)求过A、D、C三点的抛物线的解析式及其对称轴L.
(3)若P是抛物线的对称轴L上的点,那么使![]() PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
解:(1) ![]() DC∥AB,AD=DC=CB,
DC∥AB,AD=DC=CB, ![]() ∠CDB=∠CBD=∠DBA,
∠CDB=∠CBD=∠DBA,
∠DAB=∠CBA, ![]() ∠DAB=2∠DBA,
∠DAB=2∠DBA,
∠DAB+∠DBA=90![]() ,
, ![]() ∠DAB=60
∠DAB=60![]() ,
,
∠DBA=30![]() ,
,![]() AB=4,
AB=4, ![]() DC=AD=2,
DC=AD=2,
Rt![]() AOD,OA=1,OD=
AOD,OA=1,OD=![]() ,
,
![]() A(-1,0),D(0,
A(-1,0),D(0, ![]() ),C(2,
),C(2, ![]() ). 4分
). 4分
(2)根据抛物线和等腰梯形的对称性知,满足条件的抛物线必过点A(-1,0),B(3,0),
故可设所求为 ![]() =
=![]() (
(![]() +1)(
+1)( ![]() -3)
-3)
将点D(0, ![]() )的坐标代入上式得,
)的坐标代入上式得, ![]() =
=![]() .
.
所求抛物线的解析式为 ![]() =
=![]()
其对称轴L为直线![]() =1.
=1.
(3) ![]() PDB为等腰三角形,有以下三种情况:
PDB为等腰三角形,有以下三种情况:
①因直线L与DB不平行,DB的垂直平分线与L仅有一个交点P1,P1D=P1B,
![]() P1DB为等腰三角形;
P1DB为等腰三角形;
②因为以D为圆心,DB为半径的圆与直线L有两个交点P2、P3,DB=DP2,DB=DP3, ![]() P2DB,
P2DB, ![]() P3DB为等腰三角形;
P3DB为等腰三角形;
③与②同理,L上也有两个点P4、P5,使得 BD=BP4,BD=BP5.
由于以上各点互不重合,所以在直线L上,使![]() PDB为等腰三角形的点P有5个.
PDB为等腰三角形的点P有5个.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
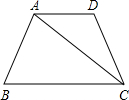 已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.
已知如图所示,在梯形ABCD中,AD∥BC,AB=AD=DC=8,∠B=60°,连接AC.查看答案和解析>>
科目:初中数学 来源: 题型:
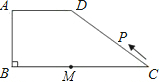 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C?D?A?B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有查看答案和解析>>
科目:初中数学 来源: 题型:
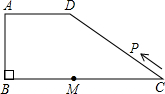 如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.
如图所示,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=6,BC=14,点M是线段BC上一定点,且MC=8.动点P从C点出发沿C→D→A→B的路线运动,运动到点B停止.在点P的运动过程中,使△PMC为等腰三角形的点P有几个?并求出相应等腰三角形的腰长.查看答案和解析>>
科目:初中数学 来源: 题型:
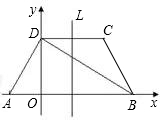 如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是
如图所示,在梯形ABCD中,已知AB∥CD,AD⊥DB,AD=DC=CB,AB=4,DO垂直于AB.则腰长是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com