
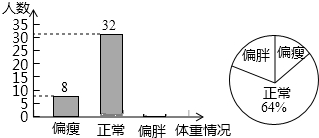
分析 (1)根据统计图可知体重正常的人数为32人,占总人数的64%,根据数据总数=频数÷百分比即可求得答案;
(2)先求得偏胖的人数,然后补全统计图即可;
(3)求得偏胖人数所占的百分比,然后七年级学生的总人数×百分比即可.
解答 解:(1)32÷64%=50(名).
答:一共调查了50名学生.
(2)50-8-32=10(名).
补全统计图如图所示.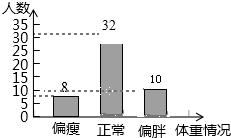
(3)10÷50=20%,800×20%=160(人).
答:该校七年级学生偏胖的大约有160人.
点评 本题主要考查的是条形统计图和扇形统计图的认识,根据统计图得出体重正常的人数为32人,占总人数的64%,然后利用频数、总数、百分比的关系求解是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
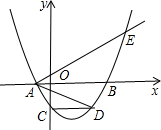 如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
如图,二次函数y=ax2-2amx-3am2(其中a、m是常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B的左侧),与y轴交于C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD,过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
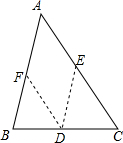 已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.
已知△ABC,试说明∠A+∠B+∠C=180°,明明给出了下列不完整的解题步骤,请你将解题过程补充完整.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com