
【题目】如图:在数轴上,点A表示a, 点B表示b, 点C表示c,b是最大的负整数,且a,c满足![]()
![]()
![]() ________,
________,![]() _________,
_________,![]() _____________
_____________
![]() 若将数轴折叠,使得
若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数____________表示的点重合;
与数____________表示的点重合;
![]() 点
点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点![]() 和点
和点![]() 分别以每秒
分别以每秒![]() 个单位长度和
个单位长度和![]() 个单位长度的速度向右运动,假设
个单位长度的速度向右运动,假设![]() 秒钟过后,
秒钟过后,
①请问:![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
②探究:若点![]() 向右运动,点
向右运动,点![]() 向左运动,速度保持不变,
向左运动,速度保持不变,![]() 的值是否随着时间
的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.

【答案】(1)-3,-1,5;(2)3;(3)①![]() 的值不随着时间
的值不随着时间![]() 的变化而改变,值为14;②当
的变化而改变,值为14;②当![]() 时,
时, ![]() 的值随着时间
的值随着时间![]() 的变化而改变;当
的变化而改变;当![]() 时,
时, ![]() 的值不随着时间
的值不随着时间![]() 的变化而改变,值为26.
的变化而改变,值为26.
【解析】
(1)根据非负数的性质即可得到结论;
(2)先求出对称点,即可得出答案;
(3)①t秒后,![]() ,
,![]() ,代入
,代入![]() 计算即可得到答案;
计算即可得到答案;
②先求出![]() ,再分当
,再分当![]() 时和当
时和当![]() 时,讨论求解即可.
时,讨论求解即可.
解:![]() ∵
∵![]() ,
,
∴a+3=0,c5=0,
解得a=3,c=5,
∵b是最大的负整数,
∴b=-1
故答案为:3,-1,5.
(2)点A与点C的中点对应的数为:![]() ,
,
点B到1的距离为2,所以与点B重合的数是:1+2=3.
故答案为:3.![]() ①t秒后,
①t秒后,![]() ,
,
![]() ,
,
![]() .
.
故![]() 的值不随着时间
的值不随着时间![]() 的变化而改变;
的变化而改变;
②![]() .
.
![]() ,
,
![]() .
.
当![]() 时,原式
时,原式![]() 的值随着时间
的值随着时间![]() 的变化而改变;
的变化而改变;
当![]() 时,原式
时,原式![]() 的值不随着时间
的值不随着时间![]() 的变化而改变.
的变化而改变.


科目:初中数学 来源: 题型:
【题目】如图,一定数量的石子可以摆成如图所示的三角形和四边形,古希腊科学家把数1,3,6,10,15,21,...称为“三角形数”;把1,4,9,25,...称为“正方形数”.同样可以把1,5,12,22,...,等数称为“五边形数”.
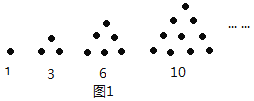
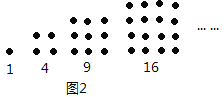
将三角形、正方形、五边形都整齐的由左到右填在所示表格里:

(1)按照规律,表格中a=_______________,b=_________________,c=________________________
(2)观察表中规律,第n个“正方形数”是_________________;若第n个“三角形数”是x,则用含x、n的代数式表示第n个“五边形数”是 ______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 中,
中,![]() 是
是![]() 的角平分线,
的角平分线,![]() 是
是![]() 的
的![]() 边上的高,过点
边上的高,过点![]() 做
做![]() ,交直线
,交直线![]() 于点
于点![]() .
.
![]() 如图1,若
如图1,若![]() ,则
,则![]() ___ ____;
___ ____;
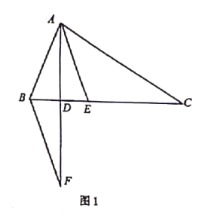
![]() 若
若![]() 中的
中的![]() ,则
,则![]() __ ____;(用
__ ____;(用![]() 表示)
表示)
![]() 如图2,
如图2,![]() 中的结论还成立吗?若成立,说明理由;若不成立,请求出
中的结论还成立吗?若成立,说明理由;若不成立,请求出![]() .(用
.(用![]() 表示)
表示)
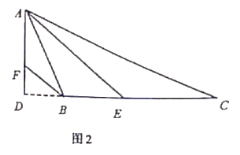
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在白纸上画两条长度均为![]() 且夹角为
且夹角为![]() 的线段
的线段![]() 、
、![]() ,然后你把一支长度也为
,然后你把一支长度也为![]() 的铅笔
的铅笔![]() 放在线段
放在线段![]() 上,将这支铅笔以线段
上,将这支铅笔以线段![]() 上的一点
上的一点![]() 为旋转中心旋转顺时针旋转一周。
为旋转中心旋转顺时针旋转一周。
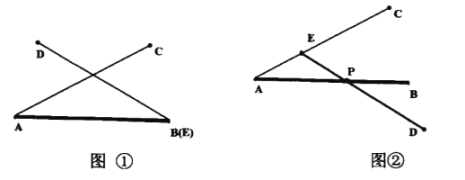
(1)若![]() 与
与![]() 重合,当旋转角为______时,这支铅笔与线段
重合,当旋转角为______时,这支铅笔与线段![]() 、
、![]() 围成的三角形是等腰三角形。
围成的三角形是等腰三角形。
(2)点![]() 从
从![]() 逐渐向
逐渐向![]() 移动,记
移动,记![]() :
:
①若![]() ,当旋转角为
,当旋转角为![]() 、______、______、______、
、______、______、______、![]() 、______时这支铅笔与线段
、______时这支铅笔与线段![]() 、
、![]() 共围成6个等腰三角形。
共围成6个等腰三角形。
②当这支铅笔与线段![]() 、
、![]() 正好围成5个等腰三角形时,求
正好围成5个等腰三角形时,求![]() 的取值范围。
的取值范围。
③当这支铅笔与线段![]() 、
、![]() 正好围成3个等腰三角形时,直接写出
正好围成3个等腰三角形时,直接写出![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,BD是它的一条对角线,过A、C两点分别作
中,BD是它的一条对角线,过A、C两点分别作![]() ,
,![]() ,E、F为垂足.
,E、F为垂足.
(1)如图,求证:![]() ;
;
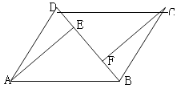
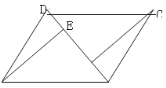
(2)如图,连接AC,设AC、BD交于点O,若![]() .在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
.在不添加任何辅助线的情况下,请直接写出图中的所有长度是OE长度2倍的线段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风“利奇马”给我县带来极端风雨天气,有一个水库8月9日8:00的水位为﹣0.1m(以10m为警戒线,记高于警戒线的水位为正)在以后的6个时刻测得的水位升降情况如下(记上升为正,单位:m)
时刻 | 1 | 2 | 3 | 4 | 5 | 6 |
升降 | 0.5 | ﹣0.4 | 0.6 | ﹣0.5 | 0.2 | ﹣0.8 |
(1)根据记录的数据,求第2个时刻该水库的实际水位;
(2)在这6个时刻中,该水库最高实际水位是多少?
(3)经过6次水位升降后,水库的水位超过警戒线了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处60![]() m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶
m的点D(点D与楼底C在同一水平面上)出发,沿斜面坡比为i=1∶![]() 的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30 m到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡比i=1∶![]() ,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.
,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25 m,与亭子距离CE=20 m.小丽从楼房顶测得点E的俯角为45°,求楼房AB的高.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校进行校园美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,如果由甲队先做20天,剩下的工程由甲、乙合作24天完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需要支付工程款3.5万元,乙队施工一天需要支付工程款2万元:如果规定在70天内完成这项工作,是由甲、乙两队单独完成省钱?还是由甲乙合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com