
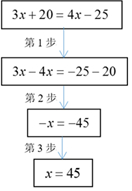
 下面的框图表示解方程3x+20=4x-25的流程.第1步的依据是等式两边加(或减)同一个数(或式子),结果仍相等.
下面的框图表示解方程3x+20=4x-25的流程.第1步的依据是等式两边加(或减)同一个数(或式子),结果仍相等. 科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.
在平面直角坐标系xOy中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),若a=|x1-x2|,b=|y1-y2|,则记作(P,Q)→{a,b }.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 日期 | 摘要 | 币种 | 存/取款金额 | 余额 | 操作员 | 备注 |
| 151101 | 北京水费 | RMB钞 | -125.45 | 874.55 | 010005B25 | 折 |
| 160101 | 北京水费 | RMB钞 | -136.02 | 738.53 | 010005Y03 | 折 |
| 160301 | 北京水费 | RMB钞 | -132.36 | 606.17 | 010005D05 | 折 |
| 160501 | 北京水费 | RMB钞 | -128.59 | 477.58 | 01000K19 | 折 |
| A. | 738.53元 | B. | 125.45元 | C. | 136.02元 | D. | 477.58元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数y=$\frac{12}{x}$(x>0)图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com