
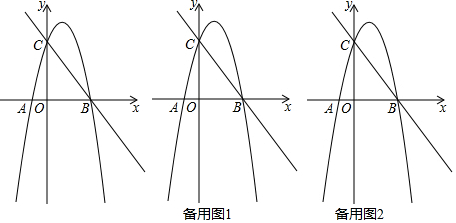
分析 (1)由直线解析式可求得B、C两点坐标,结合对称轴,可求得a、b;
(2)过点P作PE∥y轴交BC于点D,交x轴于点E,作CF⊥PD于点F,可用t表示出PD的长,则可示得S与t的关系式;
(3)当点P在x轴下方时,过点A作AH⊥CP1,利用面积相等可求得AK、CK的比,再利用勾股定理可求得K点的坐标,则可求得直线CK解析式,结合P1在抛物线上可求得其坐标;当点P在x轴上方时,过点B作BM∥y轴,交CP2延长线于点M,可证明△CBK≌△CBM,则可求得M点坐标,可求得直线CM解析式,同理可求得P2点的坐标,则可求得P点坐标.
解答 解:
(1)∵直线y=-x+3与x轴、y轴相交于B、C两点,
∴B(3,0),C(0,3),
∴9a+3b+3=0,
∵抛物线对称轴为直线x=1,
∴$-\frac{b}{2a}=1$,
∴a=-1,b=2;
(2)如图1,过点P作PE∥y轴交BC于点D,交x轴于点E,作CF⊥PD于点F,
∵P(t,-t2+2t+3),
∴D(t,-t+3),
∵点P是直线BC上方,
∴PD=-t2+2t+3-(-t+3)=-t2+3t,
∴S△PBC=S△PCD+S△PBD=$\frac{1}{2}$PD•CF+$\frac{1}{2}$PD•BE=$\frac{1}{2}$PD•OB=$\frac{1}{2}$×3(-t2+3t)=-$\frac{3}{2}$t2+$\frac{9}{2}$t(0<t<3);
(3)①如图2,当∠BCP1=∠ACO时,过点A作AH⊥CP1,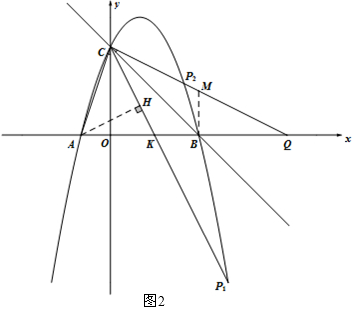
∵OA=1,OC=3,
∴AC=$\sqrt{10}$,
∵∠BCP1=∠ACO,
∴∠ACH=45°,
∴AH=$\sqrt{5}$,
∵S△ACK=$\frac{1}{2}$AK•OC=$\frac{1}{2}$CK•AH,
∴$\frac{AK}{CK}$=$\frac{AH}{OC}$=$\frac{\sqrt{5}}{3}$,
设AK=$\sqrt{5}m$,CK=3m,OK=$\sqrt{5}$m-1,
在Rt△COK中,OC2+OK2=CK2
∴${3^2}+{(\sqrt{5}m-1)^2}={(3m)^2}$32+($\sqrt{5}$m-1)2=(3m)2,解得m=$\frac{\sqrt{5}}{2}$,
∴K($\frac{3}{2}$,0),
∴直线CK解析式为y=-2x+3,
∴P1(n,-2n+3)
∵P1在抛物线y=-x2+2x+3上,
∴P1(4,-5);
②如图2,∠BCP2=∠ACO时,过点B作BM∥y轴,交CP2延长线于点M,
在△CBK和△CBM中
$\left\{\begin{array}{l}{∠BC{P}_{2}=∠BC{P}_{1}}\\{BC=BC}\\{∠CBO=∠CBM}\end{array}\right.$
∴△CBK≌△CBM(ASA),
∴BK=BM=$\frac{3}{2}$,
∴M(3,$\frac{3}{2}$),
∴直线CM的解析式为y=-$\frac{1}{2}$x+3,
∴P2(m,-$\frac{1}{2}$m+3)
∵P2在抛物线上,
∴P2($\frac{5}{2}$,$\frac{7}{4}$),
∴P点坐标为(4,-5)或($\frac{5}{2}$,$\frac{7}{4}$).
点评 本题为二次函数的综合应用,涉及待定系数法、三角形面积、勾股定理、全等三角形的判定和性质、方程思想及分类讨论思想等知识点.在(1)中利用对称轴和B点坐标得到关于a、b的方程是解题的关键,在(2)中用t表示出PD的长是解题的关键,在(3)中分别求得直线CK、CM的解析式是解题的关键.本题考查知识点较多,综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 北偏西50°方向上的一条射线 | B. | 北偏西40°方向上的一条射线 | ||
| C. | 南偏西40°方向上的一条射线 | D. | 南偏西50°方向上的一条射线 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com