Question

11．在△ABC中，CD⊥AB于点D，∠A=2∠BCD．

（1）如图1，求证：AB=AC；
（2）如图2，E是AB上一点，F是AC延长线上一点，连接CE、BF，CE=BF，求证：∠BEC=∠CFB；
（3）如图3，在（2）的条件下，作EG∥BC交AC于点G，若∠CBF=2∠ACE，EG=2，BC=6，求BF的长．

Answer 1

分析 （1）先设∠BCD=x，则∠A=2∠BCD=2x，根据CD⊥AB，求∠ABC=90°-x，∠ACB=90°-x，进而得到∠ABC=∠ACB，即可得出结论；
（2）先作BH⊥AC于H，判定△ABH≌△ACD（AAS），进而得出Rt△BHF≌Rt△CDE（HL），最后可得∠BEC=∠CFB；
（3）先延长CB至点M，使BM=EG，连接EM，并设∠ACE=α，∠CFB=β，根据AE=AG，AB=AC，得出BE=CG，再判定△EGC≌△MBE（SAS），得出EM=EC，进而判定△ECM是等边三角形，进而得出CE=CM=BM+BC=EG+BC=2+6=8，最后得到CE=BF=8．

解答 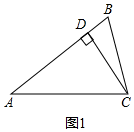解：（1）如图1，设∠BCD=x，则∠A=2∠BCD=2x，
∵CD⊥AB，
∴∠CDB=90°，
∴∠ABC=90°-x，
∵∠A=2x，
∴∠ACB=180°-2x-（90°-x）=90°-x，
∴∠ABC=∠ACB，
∴AB=AC；

（2）证明：如图2，作BH⊥AC于H，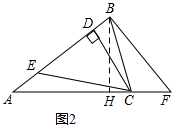
∴∠AHB=∠ADC=90°，
∵在∴△ABH和△ACD中，
$\left\{\begin{array}{l}{∠AHB=∠ADC}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$，
∴△ABH≌△ACD（AAS），
∴BH=CD，
∵∠BHF=∠EDC=90°，
∴在Rt△BHF和Rt△CDE中，
$\left\{\begin{array}{l}{CE=BF}\\{BH=CD}\end{array}\right.$，
∴Rt△BHF≌Rt△CDE（HL），
∴∠BEC=∠CFB；

（3）如图3，延长CB至点M，使BM=EG，连接EM，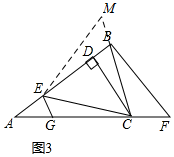
设∠ACE=α，∠CFB=β，
∴∠CBF=2∠ACE=2α，∠ACB=∠ABC=2α+β，∠BEC=∠CFB=β，
∵∠ACE=α，
∴∠ECB=α+β，
在△ECB中，α+β+β+2α+β=180°，
∴α+β=60°，
∴∠ECB=60°，
∵EG∥BC，
∴∠AEG=∠ABC，∠AGE=∠ACB，
∵∠ABC=∠ACB，
∴∠AEG=∠ABC=∠ACB=∠AGE，
∴AE=AG，
∵AB=AC，
∴AB-AE=AC-AG，
∴BE=CG，
∵∠AGE+∠EGC=180°，∠ABC+∠EBM=180°，
又∵∠AGE=∠ABC，
∴∠EGC=∠EBM，
∵BM=EG，
∴△EGC≌△MBE（SAS），
∴EM=EC，
∵∠ECB=60°，
∴△ECM是等边三角形，
∴CE=CM=BM+BC=EG+BC=2+6=8，
又∵CE=BF，
∴BF=8．

点评 本题属于三角形综合题，主要考查了全等三角形的判定与性质，三角形内角和定理以及等边三角形的判定与性质的综合应用，解决问题的关键是作辅助线构造全等三角形，依据全等三角形的对应边相等进行求解．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．