
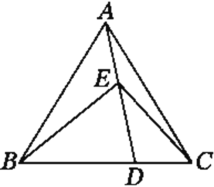
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,连接
上,连接![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() .
.
![]() 求证:四边形
求证:四边形![]() 是矩形.
是矩形.
![]() 小明在完成
小明在完成![]() 的证明后继续进行了探索,过点
的证明后继续进行了探索,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,得到四边形
,得到四边形![]() .此时,他猜想四边形
.此时,他猜想四边形![]() 是菱形.请在下列框图中补全他的证明思路.
是菱形.请在下列框图中补全他的证明思路.
小明的证明思路:由![]() ,
,![]() ,
,![]() 易证,四边形
易证,四边形![]() 是平行四边形.要证□
是平行四边形.要证□![]() 是菱形,只要证
是菱形,只要证![]() .由已知条件________,
.由已知条件________,![]() ,可证
,可证![]() ,故只要证
,故只要证![]() ,即证
,即证![]() ,易证________,________,故只要证
,易证________,________,故只要证![]() ,易证
,易证![]() ,
,![]() ,________,故得
,________,故得![]() ,即可得证.
,即可得证.

【答案】![]() 平分
平分![]()
![]()
![]()
![]()
【解析】
(1)由AB∥CD可得∠AEF=∠DFE,∠BEF=∠CFE,又由EG、FG、EH、FH均为角平分线可得DG∥FH,EH∥GF,且∠EGF=∠EHF=90°,故可得四边形EGFH为矩形;
(2)利用MN∥EF及FG是角平分线可证△NGF为等腰三角形,得NG=NF;再通过证明△MGE≌△QHF得MG=QF,从而得到NM=NQ进而证明四边形![]() 是菱形.
是菱形.
(1)证明:∵EH平分∠BEF,
∴∠FEH=![]() ∠BEF,
∠BEF,
∵FH平分∠DFE,
∴∠EFH=![]() ∠DFE,
∠DFE,
∵AB∥CD,
∴∠BEF+∠DFE=180°,
∴∠FEH+∠EFH=![]() (∠BEF+∠DFE)=
(∠BEF+∠DFE)=![]() ×180°=90°,
×180°=90°,
∵∠FEH+∠EFH+∠EHF=180°,
∴∠EHF=180°-(∠FEH+∠EFH)=180°-90°=90°,
同理可得:∠EGF=90°,
∵EG平分∠AEF,
∴∠EFG=![]() ∠AEF,
∠AEF,
∵EH平分∠BEF,
∴∠FEH=![]() ∠BEF,
∠BEF,
∵点A、E、B在同一条直线上,
∴∠AEB=180°,
即∠AEF+∠BEF=180°,
∴∠FEG+∠FEH=![]() (∠AEF+∠BEF)=
(∠AEF+∠BEF)=![]() ×180°=90°,
×180°=90°,
即∠GEH=90°
∴四边形EGFH是矩形;
(2) 答案不唯一:
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证 GE=FH、∠GME=∠FQH.
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证;
故答案为:FG平分∠CFE,GE=FH、∠GME=∠FQH,∠GEF=∠EFH.


科目:初中数学 来源: 题型:
【题目】如图,在锐角ΔABC中,已知AB=AC,D为底边BC上的一点,E为线段AD上的一点,且∠BED=∠BAC=2∠DEC,连接CE.
(1)求证:∠ABE=∠DAC
(2)若∠BAC=60°,试判断BD与CD有怎样的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑销售商试销某一品牌电脑(出厂为![]() 元/台)以
元/台)以![]() 元/台销售时,平均每月可销售
元/台销售时,平均每月可销售![]() 台,现为了扩大销售,销售商决定降价销售,在原来
台,现为了扩大销售,销售商决定降价销售,在原来![]() 月份平均销售量的基础上,经
月份平均销售量的基础上,经![]() 月份的市场调查,
月份的市场调查,![]() 月份调整价格后,月销售额达到
月份调整价格后,月销售额达到![]() 元.已知电脑价格每台下降
元.已知电脑价格每台下降![]() 元,月销售量将上升
元,月销售量将上升![]() 台.
台.
![]() 求
求![]() 月份到
月份到![]() 月份销售额的月平均增长率;
月份销售额的月平均增长率;
![]() 求
求![]() 月份时该电脑的销售价格.
月份时该电脑的销售价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图可以自由转动的转盘被![]() 等分,指针落在每个扇形内的机会均等.
等分,指针落在每个扇形内的机会均等.
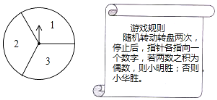
![]() 现随机转动转盘一次,停止后,指针指向数字
现随机转动转盘一次,停止后,指针指向数字![]() 的概率为________;
的概率为________;
![]() 小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
小明和小华利用这个转盘做游戏,若采用下列游戏规则,你认为对双方公平吗?请用列表或画树状图的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是售货员与小丽的对话:

根据对话内容解答下列问题:
(1)A,B两种文具的单价各是多少元?
(2)若购买A,B两种文具共20件,其中A种文具的数量少于10件,且购买总费用不超过260元,共有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是弧![]() 的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线BD于点F,AF交⊙O于点H,连接BH.
⑴求证:AC=CD.
⑵若OB=2,求BH的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com