分析:这几道题应注意换元法的运用;解决此类题如
+=+,关键是使其分母先相等或分子先相等,再使其分子或分母相等.
解答:解:(1)∵
-=0,∴(x-1)
2-2x=0,
∴
x2-4x+1=0,x1=2+,x2=2-;
2)∵
+=,
∴(x+3)(x-3)+(x+2)(x-2)=(x+1)(x-1),
∴x
2=12,∴
x1=2,x2=-2.
(3)令
y=x+,则原方程化为2y
2-3y-5=0,
∴
y1=-1,y2=,∴
x+=-1,x2+x+1=0无解,或
x+=,
∴2x
2-5x+2=0,∴
x1=2,x2=;
(4)令x
2+2x-1=y,则原方程化为
y-=2,∴y
2-2y-3=0,∴y
1=3,y
2=-1,∴x
2-2x-1=3,即x
2-2x-4=0,∴
x1=-1,x2=--1或x
2+2x-1=-1,∴x
3=0,x
4=-2.
(5)设x
2-2x-1=y,则原方程化为
+=∴(y-1)(y-2)+2y(y-2)-3y(y-1)=0,∴
4y-2=0,y=,∴
x2-2x-1=,∴2x
2-4x-3=0,
∴
x1=,x2=.
(6)∵
=,
∴
=∴10x=40,∴x=4.
(7)
+=+∴原方程化为
-=+∴
-=-∴
=∴x=8.
点评:本题主要考查用换元法解分式方程,难度较大.注意:换元法应先将方程中多次出现的一个式子设为一个字母,然后得到一个新的方程,然后解出,反代入原式即可求解.



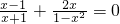 ______.
______.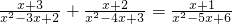 ______.
______.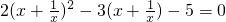 ______.
______.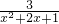 =2______.
=2______.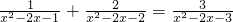 ______.
______.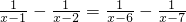 ______.
______.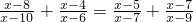 ______.
______.