下列方程的解分别是:
(1)x3-3x2+2x=0 .
(2)x4-5x2+4=0 .
(3)(x2-3x)2-2(x2-3x)-8=0 .
(4)(x2-5x-6)(x2-5x+11)=18 .
(5)(x+1)(x+2)(x-3)(x-4)=36 .
(6)(x+1)(x-1)=1 .
(7)x2-3|x|+2=0 .
(8)(x+1)(x-1)=x+1 .
(9)x2-3|x|+2=0 .
(10)x4+2x3+5x2+4x-12=0 .
【答案】
分析:(1)先分解因式再求解即可;
(2)分解因式再求解;
(3)先分解因式再求解即可;
(4)换元法即可求解;
(5)换元法即可求解;
(6)根据平方差公式即可求解;
(7)先分类讨论去绝对值即可求解;
(8)根据平方差公式即可求解;
(9)先分类讨论去绝对值即可求解;
(10)分解因式后即可求解;
解答:解:(1)x
3-3x
2+2x=0,∴x(x
2-3x+2)=0,∴x
1=0,x
2=1,x
3=2;
(2)x
4-5x
2+4=0,∴(x
2-4)(x
2-1)=0,∴x
1=2,x
2=-2,x
3=1,x
4=1;
(3)(x
2-3x)
2-2(x
2-3x)-8=0,设x
2-3x=y,
∴y
2-2y-8=0,∴(y-4)(y+2)=0,∴x
1=4,x
2=-1,x
3=1,x
4=2;
(4)∵(x
2-5x)
2+5(x
2-5x)-66=18,
∴(x
2-5x)
2+5(x
2-5x)-84=0,(x
2-5x+12)(x
2-5x-7)=0
∴x
2-5x+12=0(无解),或x
2-5x-7=0,
它的解为x
1=
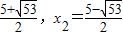
;
(5)∵(x
2-2x-3)(x
2-2x-8)=36,
∴(x
2-2x)
2-11(x
2-2x)-12=0,
∴(x
2-2x-12)(x
2-2x+1)=0,
∴x
2-2x-12=0或x
2-2x+1=0,
∴
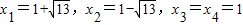
(6)(x+1)(x-1)=1∴x
1,2=
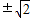
;
(7)x
2-3|x|+2=0,当x>0时,x
1=1,x
2=2;当x≤0时,x
1=-1,x
2=-2;
(8)x
2(x-2)-4(x-2)=0,(x-2)(x
2-4)=0,(x-2)
2(x+2)=0,
∴x
1=x
2=2,x
3=-2
(9)∵x
2=|x
2|=|x•x|=|x||x|=|x|
2,∴原方程为|x|
2-3|x|+2=0,∴(|x|-1)(|x|-2)=0,∴|x|-1=0或|x|=2,∴x
1=1,x
2=-1,x
3=2,x
4=-2.
(10)∵(x
4+2x
3+x
2)+(4x
2+4x)-12=0.
即(x
2+x)
2+4(x
2+x)-12=0,∴(x
2+x+6)(x
2+x-2)=0,∵
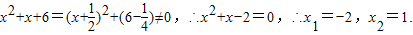 点评:
点评:本题考查了高次方程,难度一般,关键是注意细心运算即可.

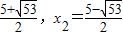 ;
;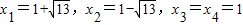
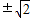 ;
;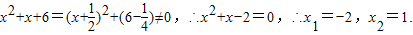


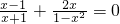 ______.
______.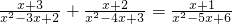 ______.
______.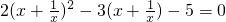 ______.
______.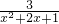 =2______.
=2______.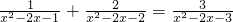 ______.
______.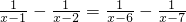 ______.
______.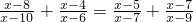 ______.
______.