Question

12．教学实验：画∠AOB的平分线OC．
（1）将一块最够大的三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别于OA，OB交于E，F（如图①）．度量PE、PF的长度，PE=PF（填＞，＜，=）；
（2）将三角尺绕点P旋转（如图②）：
①PE与PF相等吗？若相等请进行证明，若不相等请说明理由；
②若OP=$\sqrt{2}$，请直接写出四边形OEPF的面积：1．

Answer 1

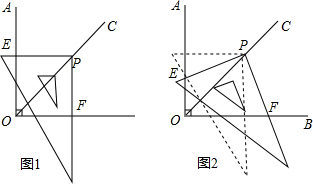
分析 （1）由题意容易得出结果；
（2）①把三角尺绕点P顺时针旋转，使三角尺的两条直角边分别与OA，OB垂直于M、N，证出四边形OMPN是正方形，由ASA证明△PEM≌△PFN，得出对应边相等即可．
②由①得出四边形OMPN是正方形，△PEM≌△PFN，由正方形的性质得出OM=ON=$\frac{\sqrt{2}}{2}$OP=1，四边形OEPF的面积=正方形OMPN的面积=OM²=1即可．

解答 （1）解：PE=PF；
     故答案为：=；
（2）解：①PE=PF；理由如下：
把三角尺绕点P顺时针旋转，使三角尺的两条直角边分别与OA，OB垂直于M、N，如图所示：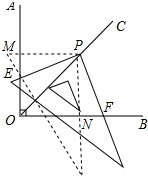
则∠PME=∠PNF=90°，四边形OMPN是矩形
∵OP平分∠AOB，
∴PM=PN，
∴四边形OMPN是正方形，
∵∠AOB=∠PME=∠PNF=90°，
∴∠MPN=90°，
∵∠EPF=90°，
∴∠MPE=∠FPN，
在△PEM和△PFN中$\left\{\begin{array}{l}∠PME=∠PNF\\ PM=PN\\∠MPE=∠NPF\end{array}\right.$
∴△PEM≌△PFN（ASA），
∴PE=PF．
②由①得：四边形OMPN是正方形，△PEM≌△PFN，
∴OM=ON=$\frac{\sqrt{2}}{2}$OP=1，四边形OEPF的面积=正方形OMPN的面积=OM²=1；
故答案为：1．

点评 本题考查了正方形的判定与性质、旋转的性质、全等三角形的判定与性质、勾股定理、正方形面积的计算；熟练掌握正方形的性质，证明三角形全等是解决问题的关键．