
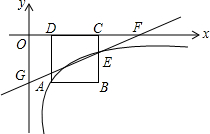
 如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0). 分析 根据点A的纵坐标求出边CD的长,得到n=m+2,解方程组求出m的值,根据待定系数法求出直线l的解析式即可得到答案.
解答 解:∵A(m,-2)在反比例函数y=$\frac{k}{x}$图象上,∴k=-2m,
∵CD=DA=2,∴n=m+2,
∴-$\frac{2}{3}$(m+2)=k,又
解得,m=1,k=-2m,
设直线l的解析式为y=kx+b,
则$\left\{\begin{array}{l}{3k+b=-\frac{2}{3}}\\{b=-2}\end{array}\right.$,解得,$\left\{\begin{array}{l}{k=\frac{4}{9}}\\{b=-2}\end{array}\right.$,
∴直线l的解析式为y=$\frac{4}{9}$x-2,
当y=0时,x=$\frac{9}{2}$,
∴点F的坐标是($\frac{9}{2}$,0).
点评 本题考查的是反比例函数与一次函数的交点问题和待定系数法的应用,掌握正方形的性质和待定系数法是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
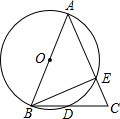 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
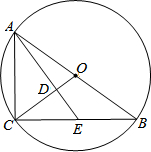 如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.
如图,⊙O是Rt△ABC的外接圆,∠ACB=90°,E为BC上一点,连接AE与OC交于点D,∠CAE=∠CBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
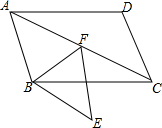 如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
如图,点F在?ABCD的对角线AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
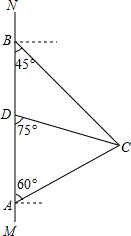 如图,在我国领海某海域,南北方向的直线MN上有相距100($\sqrt{3}$+1)海里的A、B两艘巡逻舰,同时发现C处有一艘不明国籍的战舰在从事侦查、收集情报活动,立即前往进行驱离,出发时,B舰测得敌舰所处位置C位于东南方向上,A舰测得敌舰所处位置C位于北偏东60°方向上,此时敌舰所处位置C正好位于灯塔D南偏东75°的方向上.
如图,在我国领海某海域,南北方向的直线MN上有相距100($\sqrt{3}$+1)海里的A、B两艘巡逻舰,同时发现C处有一艘不明国籍的战舰在从事侦查、收集情报活动,立即前往进行驱离,出发时,B舰测得敌舰所处位置C位于东南方向上,A舰测得敌舰所处位置C位于北偏东60°方向上,此时敌舰所处位置C正好位于灯塔D南偏东75°的方向上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
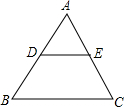 如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )
如图,D、E分别是△ABC两边的中点,△ADE的面积记为S1,四边形DBCE的面积记为S2,则下列结论正确的是( )| A. | S1=S2 | B. | S2=2S1 | C. | S2=3S1 | D. | S2=4S1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com