
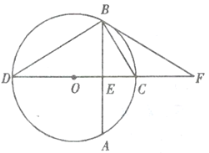
【题目】如图,![]() 的直径
的直径![]() 垂直于弦
垂直于弦![]() ,垂足为
,垂足为![]() ,
,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某种进价为每件40元的商品,通过调查发现,当销售单价在40元至65元之间(![]() )时,每月的销售量
)时,每月的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
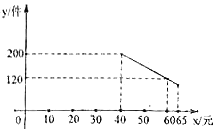
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设每月获得的利润为![]() (元),求
(元),求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)若想每月获得1600元的利润,那么销售单价应定为多少元?
(4)当销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
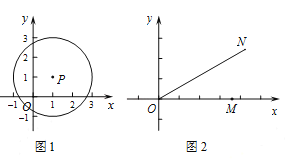
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
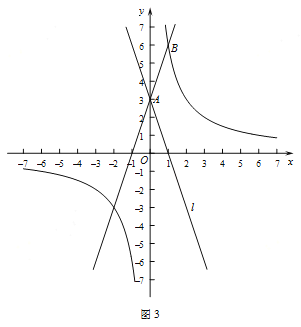
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为8,点E是正方形内部一点,连接BE,CE,且∠ABE=∠BCE,点P是AB边上一动点,连接PD,PE,则PD+PE的长度最小值为_____.
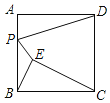
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线L:![]() 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为
经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为![]() .
.
(1)求抛物线L的表达式;
(2)点P在抛物线![]() 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=60°,OC是∠AOB的平分线,点D为OC上一点,过D作直线DE⊥OA,垂足为点E,且直线DE交OB于点F,如图所示.若DE=2,则DF=_____.
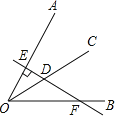
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1,若∠A=100°,求证:A1C1∥BC.
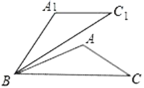
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区内从甲地到乙地的路程是![]() ,小华步行从甲地到乙地游玩,速度为
,小华步行从甲地到乙地游玩,速度为![]() ,走了
,走了![]() 后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是
后,中途休息了一段时间,然后继续按原速前往乙地,景区从甲地开往乙地的电瓶车每隔半小时发一趟车,速度是![]() ,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为
,若小华与第1趟电瓶车同时出发,设小华距乙地的路程为![]() ,第
,第![]() 趟电瓶车距乙地的路程为
趟电瓶车距乙地的路程为![]() ,
,![]() 为正整数,行进时间为
为正整数,行进时间为![]() .如图画出了
.如图画出了![]() ,
,![]() 与
与![]() 的函数图象.
的函数图象.
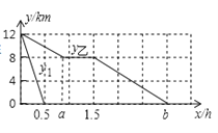
(1)观察图,其中![]() ,
,![]() ;
;
(2)求第2趟电瓶车距乙地的路程![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)当![]() 时,在图中画出
时,在图中画出![]() 与
与![]() 的函数图象;并观察图象,得出小华在休息后前往乙地的途中,共有 趟电瓶车驶过.
的函数图象;并观察图象,得出小华在休息后前往乙地的途中,共有 趟电瓶车驶过.
查看答案和解析>>
科目:初中数学 来源: 题型:
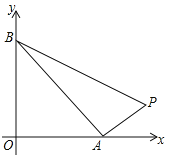
【题目】如图,由点P(14,1),A(![]() ,0),B(0,
,0),B(0,![]() )(
)(![]() ),确定的△PAB的面积为18,则
),确定的△PAB的面积为18,则![]() 的值为_________,如果
的值为_________,如果![]() ,则
,则![]() 的值为_____________________
的值为_____________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com