
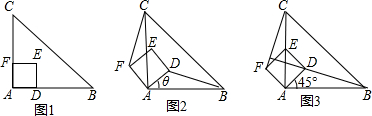
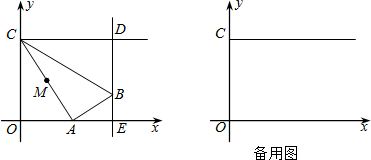
���� ��1�����ݡ�ABC�ǵ���ֱ�������Σ��ı���ADEF�������Σ����ݽDZ߽ǹ�ϵ֤����BAD�ա�CAF������ȫ�������εĶ�Ӧ����ȣ�����֤��BD=CF�����ӳ�BD��CF�ڵ�G��BG��AC�ڵ�M�����ݣ�1��֤���ġ�BAD�ա�CAF���ɵá�ABM=��GCM���ָ��ݶԶ�����ȣ��ó���BMA�ס�CMG���ٸ��ݸ������������εĶ�Ӧ����ȣ��ɵá�BGC=��BAC=90�㣬����֤��BD��CF��
��3�����ȹ���F��FN��AC�ڵ�N�����ù��ɶ����������AE��BC�ij����̶����AN��CN�ij������ɵȽǵ����Ǻ���ֵ��ȣ������AM��ֵ���Ӷ����CM��ֵ��
��� �⣺��1��BD=CF��BD��CF������
���ɣ��ߡ�ABC�ǵ���ֱ�������Σ��ı���ADEF�������Σ�
��AB=AC��AD=AF����BAC=��DAF=90�㣬
�ߡ�BAD=��BAC-��DAC����CAF=��DAF-��DAC��
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У�
$\left\{\begin{array}{l}{AB=AC}\\{��BAD=��CAF}\\{AD=AF}\end{array}\right.$
���BAD�ա�CAF��SAS����
��BD=CF��
��ͼ2���ӳ�BD��CF�ڵ�G��BG��AC�ڵ�M��
�ߡ�BAD�ա�CAF����֤����
���ABM=��GCM��
�ߡ�BMA=��CMG��
���BMA�ס�CMG��
���BGC=��BAC=90�㣮
��BD��CF��
��2����ͼ3������F��FN��AC�ڵ�N��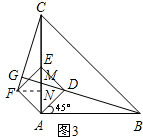
����������ADEF��AD=DE=$\sqrt{2}$��
��AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=2��
��AN=FN=$\frac{1}{2}$AE=1
���ڵ���ֱ�ǡ�ABC �У�AB=4��
��CN=AC-AN=3��BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=4$\sqrt{2}$��
����Rt��FCN��tan��FCN=$\frac{FN}{CN}=\frac{1}{3}$��
����Rt��ABM��tan��ABM=$\frac{AM}{AB}$=tan��FCN=$\frac{1}{3}$��
��AM=$\frac{1}{3}$AB=$\frac{4}{3}$��
��CM=AC-AM=4-$\frac{4}{3}$=$\frac{8}{3}$��
���� ���⿼�����ı��ε��ۺϣ��õ���֪ʶ�������������ε��ж������ʡ�ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ����ε����ʡ����ɶ����Լ����Ǻ�����֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ�ע�����ν��˼��Ӧ�ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ�����ȱߡ�ABC�Ķ���A��B��C������AB��BC��CA�Ĵ���Χ�ɡ�A1B1C1���ٹ���A1B1C1�Ķ���A1��B1��C1������A1B1��B1C1��A1C1�Ĵ���Χ�ɡ�A2B2C2�����մ˹���ֱ�����ɡ�AnBnCn����S��ABC=S����S${\;}_{��{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS��
��ͼ��ʾ�����ȱߡ�ABC�Ķ���A��B��C������AB��BC��CA�Ĵ���Χ�ɡ�A1B1C1���ٹ���A1B1C1�Ķ���A1��B1��C1������A1B1��B1C1��A1C1�Ĵ���Χ�ɡ�A2B2C2�����մ˹���ֱ�����ɡ�AnBnCn����S��ABC=S����S${\;}_{��{A}_{n}}$${\;}_{{B}_{n}}$${\;}_{{C}_{n}}$=3nS���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
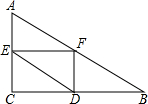 ��֪����Rt��ABC�У���C=90�㣬AC=6��BC=8����E�DZ�AC��һ���㣬����E��EF��BC����AB���ڵ�F����DΪBC����һ�㣬����DE��DF����EC�ij�Ϊx�����DEF�����y����x�ĺ�����ϵ����Ϊ��������
��֪����Rt��ABC�У���C=90�㣬AC=6��BC=8����E�DZ�AC��һ���㣬����E��EF��BC����AB���ڵ�F����DΪBC����һ�㣬����DE��DF����EC�ij�Ϊx�����DEF�����y����x�ĺ�����ϵ����Ϊ��������| A�� | 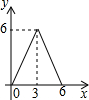 | B�� | 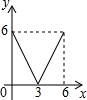 | C�� | 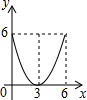 | D�� | 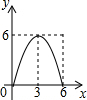 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
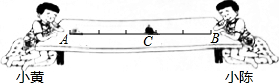 ��ͼ��С�ƺ�С�¹۲���ţ���У���ţ����AΪ�����ֱ����������B��Ĺ����У�����C��ʱ����6���ӣ���ô����Ҫ�ʱ����ܵ���B�㣿
��ͼ��С�ƺ�С�¹۲���ţ���У���ţ����AΪ�����ֱ����������B��Ĺ����У�����C��ʱ����6���ӣ���ô����Ҫ�ʱ����ܵ���B�㣿�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com