
| A. | 4cm或8cm | B. | 4cm或6cm | C. | 6cm | D. | $\sqrt{32}$cm |
分析 首先确定等腰三角形的底边的长度,再由勾股定理计算即可.
解答 解:当4为等腰三角形的腰长时,底边长=16-4-4=8,4、4、8不能构成三角形;
当4为等腰三角形的底边长时,则这个等腰三角形的底边长为4,
所以等腰三角形的三边长分别是6,6,4,
所以该等腰三角形底长上的高=$\sqrt{{6}^{2}-{2}^{2}}$=$\sqrt{32}$cm=4$\sqrt{2}$cm,
故选D
点评 本题考查了勾股定理、等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要,也是解题的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 变为原来的3倍 | B. | 变为原来的6倍 | C. | 变为原来的9倍 | D. | 不变 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
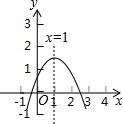 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:
我市某中学七、八年级各选派10名选手参加学校举办的环保知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀,这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表(不完整)如下所示:| 队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | m | 3.41 | 90% | 20% | |
| 八年级 | 7.1 | n | 80% | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com