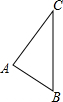
如图所示.在直角三角形ABC中.已知AB=3cm.AC=4cm.BC=5cm.现将三角形ABC沿着垂直于BC的方向平移6cm.到三角形A′B′C′的位置．(1)作出平移后的△A′B′C′,(2)求△ABC扫过的面积．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

5．

如图所示，在直角三角形ABC中，已知AB=3cm，AC=4cm，BC=5cm，现将三角形ABC沿着垂直于BC的方向平移6cm，到三角形A′B′C′的位置．
（1）作出平移后的△A′B′C′；
（2）求△ABC扫过的面积．

分析（1）利用平移的性质得出对应点位置进而求出即可；
（2）利用平移后的图形进而利用矩形面积求法得出即可．

解答解：（1）如图所示：△A′B′C′即为所求；

（2）△ABC扫过的面积为：6×BC=30（cm²）．

点评此题主要考查了平移的性质以及矩形面积求法，得出平移后对应点位置是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：选择题

9．

如图，直线l上有三个正方形A、B、C，若正方形A、C的面积分别为5和11，则正方形B的面积为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．在Rt△ABC中，∠C=90°，以三边为边分别向外作正方形，如图所示，过C作CH⊥AB于H，延长CH交MN于点I．
（1）如图（1）若AC=3$\sqrt{2}$，BC=2$\sqrt{3}$，试通过计算证明：四边形AHIN的面积等于正方形AEFC的面积．
（2）请利用图（2）证明直角三角形勾股定理：AC²+BC²=AB²．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．△ABC中，∠ACB=90°，∠A=30°，AC=$\sqrt{3}$，将△ABC绕点C顺时针旋转α，
（1）当点B的对应点B′恰好落在AB边上时（如图），α=60°；
（2）在（1）的条件下，将旋转后的图形沿射线CB平移，设平移的距离为x，平移后的图形与△ABC重叠部分的面积为y，求y与x的函数关系式，并直接写出x的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．如图1，AB∥CD，在AB、CD内有一条折线EPF．
（1）求证：∠AEP+∠CFP=∠EPF．
（2）如图2，已知∠BEP的平分线与∠DFP的平分线相交于点Q，试探索∠EPF与∠EQF之间的关系．
（3）如图3，已知∠BEQ=$\frac{1}{3}$∠BEP，∠DFQ=$\frac{1}{3}$∠DFP，则∠P与∠Q有什么关系，说明理由．
（4）已知∠BEQ=$\frac{1}{n}$∠BEP，∠DFQ=$\frac{1}{n}$∠DFP，有∠P与∠Q的关系为∠P+n∠Q=360°．（直接写结论）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．在△ABC中，AB=AC=$\sqrt{5}$，BC=4，以AC为边向△ABC外作等腰直角三角形ACD，请画出符合条件的图形，并直接写出△BCD的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

17．下列选项的值介于0.2与0.3之间的是（　　）

A．

$\sqrt{4.84}$

B．

$\sqrt{0.484}$

C．

$\sqrt{0.0484}$

D．

$\sqrt{0.00484}$

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

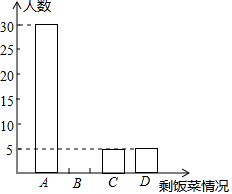自从2012年12月4日中央公布“八项规定”以来，我市某中学积极开展“厉行勤俭节约，反对铺张浪费”的活动．为此，校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查，调查内容分为四种：A．饭和菜全部吃完；B．有剩饭但菜吃完；C．饭吃完但菜有剩；D．饭和菜都有剩．学生会根据统计结果绘制了如下统计表和统计图，根据所提供的信息回答下列问题：

选项	频数	频率
A	30	M
B	n	0.2
C	5	0.1
D	5	0.1

（1）这次被抽查的学生有多少人？
（2）求表中m，n的值，并补全条形统计图；
（3）该中学有学生2200名，请估计这餐晚饭有剩饭的学生人数，按平均每人剩10克米饭计算，这餐晚饭将浪费多少千克米饭？

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

15．

如图，AD是△ABC的一条中线，若BD=3，则BC=6．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学