
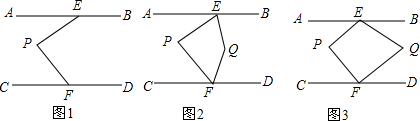
���� ��1�����ȹ���P��PG��AB��Ȼ�����AB��CD��PG��CD���ɵá�AEP=��1����CFP=��2���ݴ��жϳ���AEP+��CFP=��EPF���ɣ�
��2�������ɣ�1�����ɵá�EPF=��AEP+CFP����EQF=��BEQ+��DFQ��Ȼ����ݡ�BEP��ƽ�������DFP��ƽ�����ཻ�ڵ�Q���Ƶá�EQF=$\frac{1}{2}����360��-��EPF��$�������жϳ���EPF+2��EQF=360�㣮
��3�������ɣ�1�����ɵá�P=��AEP+CFP����Q=��BEQ+��DFQ��Ȼ����ݡ�BEQ=$\frac{1}{3}$��BEP����DFQ=$\frac{1}{3}$��DFP���Ƶá�Q=$\frac{1}{3}$����360��-��P���������жϳ���P+3��Q=360�㣮
��4�������ɣ�1�����ɵá�P=��AEP+CFP����Q=��BEQ+��DFQ��Ȼ����ݡ�BEQ=$\frac{1}{n}$��BEP����DFQ=$\frac{1}{n}$��DFP���Ƶá�Q=$\frac{1}{n}$����360��-��P���������жϳ���P+n��Q=360�㣮
��� ��1��֤������ͼ1������P��PG��AB��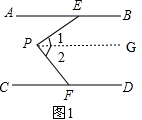 ��
��
��AB��CD��
��PG��CD��
���AEP=��1����CFP=��2��
�֡ߡ�1+��2=��EPF��
���AEP+��CFP=��EPF��
��2����ͼ2��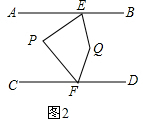 ��
��
�ɣ�1�����ɵ�
��EPF=��AEP+CFP����EQF=��BEQ+��DFQ��
�ߡ�BEP��ƽ�������DFP��ƽ�����ཻ�ڵ�Q��
���EQF=��BEQ+��DFQ=$\frac{1}{2}$����BEP+��DFP��=$\frac{1}{2}[360��-����AEP+��CFP��]$=$\frac{1}{2}����360��-��EPF��$��
���EPF+2��EQF=360�㣮
��3����ͼ3��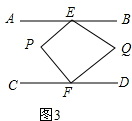 ��
��
�ɣ�1�����ɵ�
��P=��AEP+CFP����Q=��BEQ+��DFQ��
�ߡ�BEQ=$\frac{1}{3}$��BEP����DFQ=$\frac{1}{3}$��DFP��
���Q=��BEQ+��DFQ=$\frac{1}{3}$����BEP+��DFP��=$\frac{1}{3}$[360��-����AEP+��CFP��]=$\frac{1}{3}$����360��-��P����
���P+3��Q=360�㣮
��4���ɣ�1�����ɵ�
��P=��AEP+CFP����Q=��BEQ+��DFQ��
�ߡ�BEQ=$\frac{1}{n}$��BEP����DFQ=$\frac{1}{n}$��DFP��
���Q=��BEQ+��DFQ=$\frac{1}{n}$����BEP+��DFP��=$\frac{1}{n}$[360��-����AEP+��CFP��]=$\frac{1}{n}$����360��-��P����
���P+n��Q=360�㣮
�ʴ�Ϊ����P+n��Q=360�㣮
���� ������Ҫ������ƽ���ߵ����ʵ�Ӧ�ã�Ҫ�������գ�������Ĺؼ���Ҫ��ȷ����1������1������ƽ���߱�������ֱ�����أ�ͬλ����ȣ���˵�ɣ���ֱ��ƽ�У�ͬλ����ȣ���2������2������ƽ���߱�������ֱ�����أ�ͬ���ڽǻ�������˵�ɣ���ֱ��ƽ�У�ͬ���ڽǻ�������3������3������ƽ���߱�������ֱ�����أ��ڴ�����ȣ� ��˵�ɣ���ֱ��ƽ�У��ڴ�����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y��-6 | B�� | 2��y��6 | C�� | -6��y��-2 | D�� | y��-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6��7֮�� | B�� | 7��8֮�� | C�� | 8��9֮�� | D�� | 9��10֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
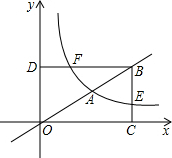 ��ͼ��A��2��1���Ǿ���OCBD�ĶԽ���OB�ϵ�һ�㣬��E��BC�ϣ�˫����y=$\frac{k}{x}$������A����BC�ڵ�E����BD�ڵ�F����CE=$\frac{2}{3}$��
��ͼ��A��2��1���Ǿ���OCBD�ĶԽ���OB�ϵ�һ�㣬��E��BC�ϣ�˫����y=$\frac{k}{x}$������A����BC�ڵ�E����BD�ڵ�F����CE=$\frac{2}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
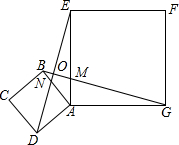 ��ͼ��������ABCD��������AEFG�й�������A������BG��ED���ڵ�O������BG��ED֮��Ĺ�ϵ����֤����IJ��룮
��ͼ��������ABCD��������AEFG�й�������A������BG��ED���ڵ�O������BG��ED֮��Ĺ�ϵ����֤����IJ��룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
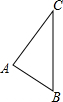 ��ͼ��ʾ����ֱ��������ABC�У���֪AB=3cm��AC=4cm��BC=5cm���ֽ�������ABC���Ŵ�ֱ��BC�ķ���ƽ��6cm����������A��B��C���λ�ã�
��ͼ��ʾ����ֱ��������ABC�У���֪AB=3cm��AC=4cm��BC=5cm���ֽ�������ABC���Ŵ�ֱ��BC�ķ���ƽ��6cm����������A��B��C���λ�ã��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-5��b-5 | B�� | 2+a��2+b | C�� | 3a��3b | D�� | $\frac{a}{3}$��$\frac{b}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com