
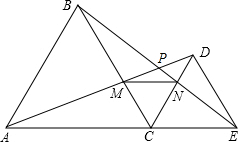
 如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:
如图,点C为线段AE上任意一点,在AE同侧分别作等边三角形△ABC和等边三角形△CDE,连接AD,BE分别交BC,CD于点M,N,连接MN,则下列结论:| A. | ①②③④⑤ | B. | ①③④⑤ | C. | ①②④⑤ | D. | ①②③⑤ |
分析 由△ACD≌△BCE得AD=BE、∠CBE=∠DAC知①正确,加之∠ACB=∠DCE=60°,AC=BC,得到△CNB≌△CMA(ASA),再根据∠MCN=60°推出△CMN为等边三角形,又由∠MNC=∠DCE,根据内错角相等,两直线平行,可知③⑤正确;根据△CNB≌△CMA(ASA),可知②正确;利用等边三角形的性质,BC∥DE,再根据平行线的性质得到∠CBE=∠DEP,于是∠APB=∠DAC+∠BEC=∠BEC+∠DEP=∠DEC=60°,可知④正确;
解答 解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD与△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$
∴△ACD≌△BCE(SAS),
∴∠CBE=∠DAC,AD=BE,故①正确;
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACM=∠BCN,
在△CNB和△CMA中,
∵$\left\{\begin{array}{l}{∠CAM=∠CBN}\\{AC=BC}\\{∠ACM=∠BCN}\end{array}\right.$,
∴△CNB≌△CMA(ASA),
∴CM=CN,
又∵∠MCN=60°可知△CMN为等边三角形,故⑤正确;
∴∠MNC=∠DCE=60°,
∴MN∥AE,故③正确,
∵△CNB≌△CMA,
∴AM=BN,故②正确;
∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
∵等边△DCE,∠EDC=60°=∠BCD,
∴BC∥DE,
∴∠CBE=∠DEP,
∴∠APB=∠DAC+∠BEC=∠BEC+∠DEP=∠DEC=60°,
∴∠APE=120°,故④正确.
正确的有:①②③④⑤.
故选:A.
点评 本题考查了等边三角形的判定与性质、全等三角形的判定与性质,根据全等三角形的判定与性质找到不变量,是解题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题.
已知A、B两地相距40km,甲、乙两人沿同一公路从A地出发到B地,甲骑摩托车,乙骑自行车,图中CD、OE分别表示甲、乙离开A地的路程y(km)与时间x(h)的函数关系的图象,结合图象解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com