
如图已知二次函数图象的顶点为原点, 直线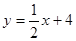 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.
(1)求这个二次函数的解析式与B点坐标;
(2) 为线段
为线段 上的一个动点(点
上的一个动点(点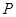 与
与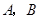 不重合),过
不重合),过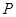 作
作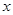 轴的垂线与这个二次函数的图象交于D点,与
轴的垂线与这个二次函数的图象交于D点,与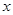 轴交于点E.设线段PD的长为
轴交于点E.设线段PD的长为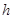 ,点
,点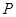 的横坐标为t,求
的横坐标为t,求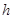 与t之间的函数关系式,并写出自变量t的取值范围;
与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段 上是否存在点
上是否存在点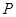 ,使得以点P、D、B为顶点的三角形与
,使得以点P、D、B为顶点的三角形与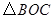 相似?若存在,请求出
相似?若存在,请求出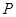 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.


解:(1)设二次函数的解析式为 ,因为A(8,8)在抛物线上,所以
,因为A(8,8)在抛物线上,所以 ,
,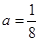 。
。
从而抛物线的解析式为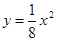 .由于直线
.由于直线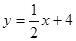 与y轴交于点B,所以B(0,4).
与y轴交于点B,所以B(0,4).
(2) 由于点P在直线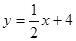 上,所以P(t,
上,所以P(t,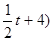 .因为PD⊥x轴,点D在抛物线上,
.因为PD⊥x轴,点D在抛物线上,
所以D(t,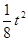 ),所以
),所以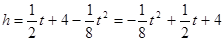 .若点P与点A重合,则t=8,若P与B重合,则t=0.所以0<t<8。
.若点P与点A重合,则t=8,若P与B重合,则t=0.所以0<t<8。
(3)过点B作x轴的平行线,交抛物线于点D1,过D1作x轴的垂线交直线AB于点P1,则
△P1D1B∽△BOC,此时D1的坐标为(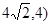 ,P1(
,P1(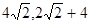 )。若过点B作AB的垂线交
)。若过点B作AB的垂线交
抛物线于点D2,作D2P2∥y轴,则△P2D2B∽△BCO,此时B(0,4),D2(t,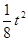 ),P2(
),P2(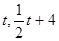 )。BP2=
)。BP2= ,P2D2=
,P2D2=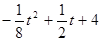 ,由于
,由于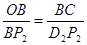 ,即
,即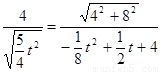 ,解得:t1=
,解得:t1=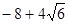 ,t2=
,t2=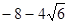 ,∵t>0,∴t=
,∵t>0,∴t=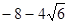 ,此时P2(
,此时P2(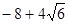 ,2
,2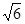 )。综上所述,满足条件的P的坐标是P(
)。综上所述,满足条件的P的坐标是P(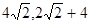 )或P(
)或P(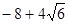 ,2
,2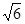 )。
)。
【解析】(1)根据抛物线的图象特征设出适当的函数关系式,由 (8,8)利用待定系数法可得二次函数的解析式,在
(8,8)利用待定系数法可得二次函数的解析式,在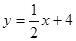 中当x=0时就得到y轴的交点为B的坐标;
中当x=0时就得到y轴的交点为B的坐标;
(2)PD的长等于点P的纵坐标减去点D的纵坐标,即得到 与t之间的函数关系式,且点P在线段AB上就可得到自变量t的取值范围;
与t之间的函数关系式,且点P在线段AB上就可得到自变量t的取值范围;
(3)根据相似三角形的对应边成比例及勾股定理可求得点的坐标。


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:内蒙古自治区中考真题 题型:解答题


查看答案和解析>>
科目:初中数学 来源:2013届海南洋浦中学九年级上期末考试数学试卷(带解析) 题型:解答题
如图已知二次函数图象的顶点为原点,直线 的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.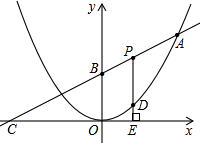
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设线段PD的长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段AB上是否存在点P,使得以点P、D、B为顶点的三角形与△BOC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年湖北省武汉市武昌区七校联考九年级(上)期中数学试卷(解析版) 题型:解答题
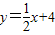 的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年海南洋浦中学九年级上期末考试数学试卷(解析版) 题型:解答题
如图已知二次函数图象的顶点为原点,直线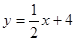 的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
的图象与该二次函数的图象交于A点(8,8),直线与x轴的交点为C,与y轴的交点为B.
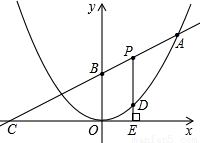
(1)求这个二次函数的解析式与B点坐标;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设线段PD的长为h,点P的横坐标为t,求h与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段AB上是否存在点P,使得以点P、D、B为顶点的三角形与△BOC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com