
【题目】如图,四边形![]() 内接于
内接于![]() ,
,![]() 平分
平分![]() .
.
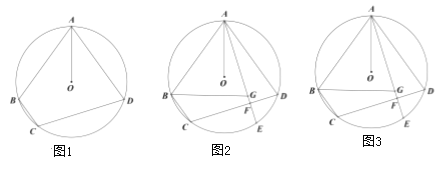
(1)如图1,求证:![]() ;
;
(2)如图2,![]() ,弦
,弦![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(3)如图3,在(2)的条件下,点![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
【答案】(1)见详解;(2)见详解;(3)![]() .
.
【解析】
(1)作OM⊥AB于M,ON⊥AD与N,由角平分线定理得到OM=ON,然后即可得到AB=AD;
(2)在FC上截取CP=BC,连接AP、AC,由CF![]() BC=DF,得到PF=DF,然后证明△ABC≌△APC,得到AB=AP=AD,由等腰三角形三线合一定理,即可得到结论;
BC=DF,得到PF=DF,然后证明△ABC≌△APC,得到AB=AP=AD,由等腰三角形三线合一定理,即可得到结论;
(3)作BT∥CD,分别交AD、AE于点T、H,则∠ATB=∠D,根据平行四边形性质,得到边的关系,然后求出AT=3,然后证明△AHT∽△BHG,得到![]() ,然后根据线段的比例关系,得到
,然后根据线段的比例关系,得到![]() ,
,![]() ,进而求出AG的长度.
,进而求出AG的长度.
(1)证明:如图1,作OM⊥AB于M,ON⊥AD与N,
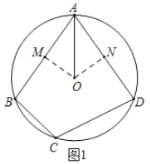
∵![]() 平分
平分![]() ,
,
∴OM=ON,
∴AM=AN,
∴AB=AD;
(2)证明:如图2,在FC上截取CP=BC,连接AP、AC,
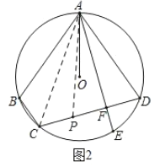
∵CF![]() CP=PF,则CF
CP=PF,则CF![]() BC=PF,
BC=PF,
∵CF![]() BC=DF,
BC=DF,
∴PF=DF,
∵AB=AD,
∴∠ACB=∠ACD,
∵CP=BC,AC=AC,
∴△ABC≌△APC(SAS),
∴AB=AP=AD,
∵PF=DF,
∴AE⊥CD(三线合一);
(3)解:如图3,作BT∥CD,分别交AD、AE于点T、H,则∠ATB=∠D,
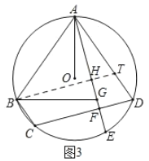
∵![]() ,
,
∴AB=CD,![]() ,
,
∴∠BAD=∠D,
∵∠ABC+∠D=180°,
∴∠ABC+∠BAD=180°,
∴AD∥BC,
∴TD=BC,BT=CD,
∵CF![]() BC=DF,
BC=DF,
∴TD=BC= CF![]() DF=CD
DF=CD![]() 2DF,
2DF,
∵![]() ,
,
∴TD=CD![]() ,
,
∴AT=AD![]() TD=CD
TD=CD![]() TD=CD
TD=CD![]() (CD
(CD![]() )=3;
)=3;
∵AE⊥CD,BT∥CD,
∴∠D+∠DAE=90°,AE⊥BT,
∴∠AGB+∠DAE=90°,
∴∠AGB=∠D,
∴∠AGB=∠ATB,
∴△AHT∽△BHG,
∴![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,
,
∴AD=BT=![]() ,
,
∴TH=BT![]() BH=
BH=![]() ,
,
∵BT∥CD,
∴![]() ,即
,即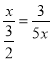 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
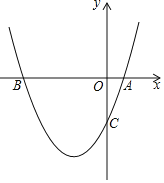
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式及顶点坐标.
(2)设点P是该抛物线上的动点,当△ABP的面积等于△ABC面积的![]() 时,求出点P的坐标.
时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ABC=90°,点D在BC的延长线上,且BD=AB,过B作BE![]() AC,与BD的垂线DE交于点E,
AC,与BD的垂线DE交于点E,
(1)求证:△ABC≌△BDE
(2)三角形BDE可由三角形ABC旋转得到,利用尺规作出旋转中心O(保留作图痕迹,不写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产厂家去年销往农村的某品牌洗碗机每台的售价![]() (元)与月份
(元)与月份![]() 之间满足函数关系
之间满足函数关系![]() ,去年的月销售量户(万台)与月份
,去年的月销售量户(万台)与月份![]() 之间成一次函数关系,其中两个月的销售情况如表:
之间成一次函数关系,其中两个月的销售情况如表:
月份: | 1月 | 5月 |
销售量: | 3.9万台 | 4.3万台 |
(1)求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?(提示:销售金额=销量×售价)
(2)经统计和计算.得到此洗碗机在农村地区的销售数据,如表:
销售数据信息表 | 售价(元/台) | 销量(万台) | 补贴金额(万元) |
去年12月份 | 2000 | 5 | / |
今年2月份 |
|
| / |
今年3月份 |
|
| 312 |
由于国家实施“家电下乡政策”,所以今年3月份国家按该产品售价的13%给子财政补贴,共补贴了312万元,从表格中,我们可以看出:今年3月份与今年2月份相比较,售价保持不变,但销量增加了1.5万台.今年2月份与去年12月份相比较,售价下降了![]() %,销量下降了1.5
%,销量下降了1.5![]() %;请用
%;请用![]() 表示表格中的
表示表格中的![]() ,
,![]() ,并根据已知条件求出
,并根据已知条件求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
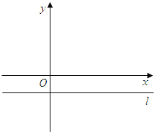
【题目】已知二次函数图象的顶点在原点![]() ,对称轴为
,对称轴为![]() 轴.一次函数
轴.一次函数![]() 的图象与二次函数的图象交于
的图象与二次函数的图象交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() 点坐标为
点坐标为![]() .平行于
.平行于![]() 轴的直线
轴的直线![]() 过
过![]() 点.
点.
![]() 求一次函数与二次函数的解析式;
求一次函数与二次函数的解析式;
![]() 判断以线段
判断以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
![]() 把二次函数的图象向右平移
把二次函数的图象向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位
个单位![]() ,二次函数的图象与
,二次函数的图象与![]() 轴交于
轴交于![]() ,
,![]() 两点,一次函数图象交
两点,一次函数图象交![]() 轴于
轴于![]() 点.当
点.当![]() 为何值时,过
为何值时,过![]() ,
,![]() ,
,![]() 三点的圆的面积最小?最小面积是多少?
三点的圆的面积最小?最小面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,C、D为
的直径,C、D为![]() 上两点,且
上两点,且![]() ,垂足为F,直线CF交AB的延长线于点E,连接AC
,垂足为F,直线CF交AB的延长线于点E,连接AC
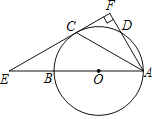
(1)判断EF与![]() 的位置关系,并说明理由:
的位置关系,并说明理由:
(2)若![]() ,
,![]() 的半径为4,求线段CF的长.
的半径为4,求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代著名数学经典,其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道长1尺.如图,已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
寸,(注:1尺=10寸)问这块圆柱形木材的直径是( )
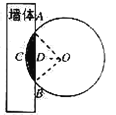
A.13寸B.6.5寸C.20寸D.26寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com