
如图,在平面直角坐标系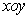 中,⊙A与y轴相切于点
中,⊙A与y轴相切于点 ,与x轴相交于M、N两点.如果点M的坐标为
,与x轴相交于M、N两点.如果点M的坐标为 ,求点N的坐标.
,求点N的坐标.

科目:初中数学 来源: 题型:
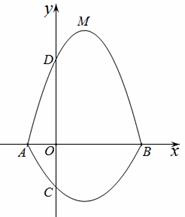
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上两点,经过A、C、B的抛物线的一部分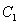 与经过点A、D、B的抛物线的一部分
与经过点A、D、B的抛物线的一部分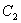 组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,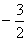 ),点M是抛物线
),点M是抛物线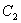 :
: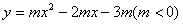 的顶点.
的顶点.
(1)求A、B两点的坐标.
(2)“蛋线 ”在第四象限上是否存在一点P,使得
”在第四象限上是否存在一点P,使得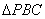 的面积最大?若存在,求出
的面积最大?若存在,求出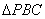 面积的最大值;若不存在,请说明理由;
面积的最大值;若不存在,请说明理由;
(3)当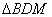 为直角三角形时,直接写出m的值.______
为直角三角形时,直接写出m的值.______
查看答案和解析>>
科目:初中数学 来源: 题型:
课外活动小组 测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是
测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB在地面上的影长BC为24米,那么旗杆AB的高度约是
A.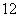 米 B.
米 B.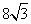 米 C.
米 C. 米 D.
米 D.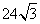 米 x k b 1 . c o m
米 x k b 1 . c o m
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数y = x2 – kx + k – 1( k>2).
(1)求证:抛物线y = x2 – kx + k - 1( k>2)与x轴必有两个交点;
(2)抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,若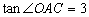 ,求抛物线的表达式;
,求抛物线的表达式;
(3)以(2)中的抛物线上一点P(m,n)为圆心,1为半径作圆,直接写出:当m取何值时,x轴与 相离、相切、相交.
相离、相切、相交.
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y= (x -1)2 +3向左平移1个单位,再向下平移3个单位后所得抛物线的
解析式为
A.y= (x -2)2 B.y=x2 C.y=x2 +6 D.y= (x -2)2 +6
查看答案和解析>>
科目:初中数学 来源: 题型:
理解与应用
小明在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第37页遇到这样一道题:
如图1,在△ABC中,P是边AB上的一点,联结CP.
要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.
请回答:
(1)小明补充的条件是____________________,或_________________.
(2)请你参考上面的图形和结论,探究、解答下面的问题:
如图2,在 △ABC中,∠A=60°,AC2= AB2+AB.BC.
△ABC中,∠A=60°,AC2= AB2+AB.BC.
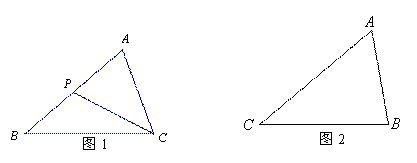 求∠B的度数.
求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=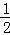 x2﹣
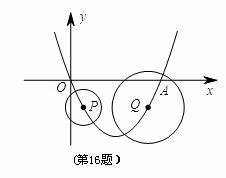
x2﹣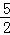 x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)
x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.若⊙P与⊙Q相离,则t的取值范围是_____ ____ .(根据2013金华模拟改编)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com