
【题目】利川市南门大桥是上世纪90年代修建的一座石拱桥,其主桥孔的横截面是一条抛物线的一部分,2019年在维修时,施工队测得主桥孔最高点![]() 到水平线
到水平线![]() 的高度为
的高度为![]() .宽度
.宽度![]() 为
为![]() .如图所示,现以
.如图所示,现以![]() 点为原点,
点为原点,![]() 所在直线为
所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
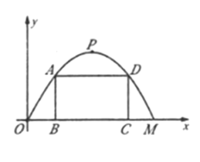
(1)直接写出点![]() 及抛物线顶点
及抛物线顶点![]() 的坐标;
的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在主桥孔内搭建矩形“脚手架”![]() ,使
,使![]() 点在抛物线上,
点在抛物线上,![]() 点在水平线
点在水平线![]() 上,为了筹备材料,需求出“脚手架”三根钢管
上,为了筹备材料,需求出“脚手架”三根钢管![]() 的长度之和的最大值是多少?请你帮施工队计算.
的长度之和的最大值是多少?请你帮施工队计算.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)三根钢管
;(3)三根钢管![]() 的长度之和的最大值是
的长度之和的最大值是![]() .
.
【解析】
(1)根据题意,即可写出点![]() 及抛物线顶点
及抛物线顶点![]() 的坐标;
的坐标;
(2)抛物线过原点![]() ,故设抛物线为
,故设抛物线为![]() ,将M和P的坐标代入即可求出抛物线的解析式;
,将M和P的坐标代入即可求出抛物线的解析式;
(3)设![]() ,分别用含x的式子表示出
,分别用含x的式子表示出![]() 的长度,设“脚手架”三根钢管
的长度,设“脚手架”三根钢管![]() 的长度之和为
的长度之和为![]() ,即可求出
,即可求出![]() 与x的函数关系式,最后利用二次函数求最值即可.
与x的函数关系式,最后利用二次函数求最值即可.
解:(1)由题意可知:![]() 抛物线顶点
抛物线顶点![]() ;
;
(2)抛物线过原点![]() ,故设抛物线为
,故设抛物线为![]() ,
,
由![]() 在抛物线上有
在抛物线上有
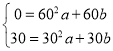 ,解得
,解得 ,
,
所以抛物线的函数解析式为![]() ,由图象可知
,由图象可知![]() ;
;
(3)设![]() ,
,
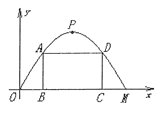
根据点A在抛物线上和矩形的性质可得
![]() ,
,
∵点A和点D关于抛物线的对称轴对称
∴点D的坐标为(60-x,y)
∴![]()
设“脚手架”三根钢管![]() 的长度之和为
的长度之和为![]() ,则
,则
![]() ,
,
即![]()
当![]() 时,
时,![]() ,
,
所以,三根钢管![]() 的长度之和的最大值是
的长度之和的最大值是![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
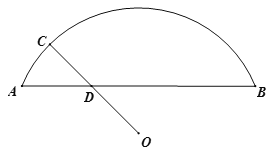
【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
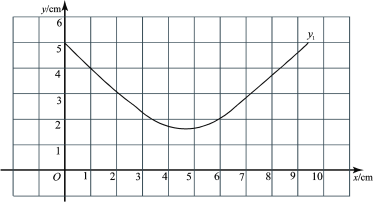
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E是AD边的中点,BD,CE交于点H,BE、AH交于点G,则下列结论:①∠ABE=∠DCE;②AG⊥BE;③S△BHE=S△CHD;④∠AHB=∠EHD.其中正确的是( )
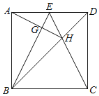
A.①③B.①②③④C.①②③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(-3,0),其对称轴为直线x=-1,有下列结论:①abc<0;②a-b-2c>0;③关于![]() 的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若
的方程ax2+(b-m)x+c=m有两个不相等的实数根;④若![]() ,
,![]() 是抛物线上两点,且
是抛物线上两点,且![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
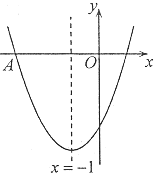
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=a与抛物线![]() 交于A、B两点(A在B的左侧),交y轴于点C
交于A、B两点(A在B的左侧),交y轴于点C
(1)若AB=4,求a的值
(2)若抛物线上存在点D(不与A、B重合),使![]() ,求a的取值范围
,求a的取值范围
(3)如图2,直线y=kx+2与抛物线交于点E、F,点P是抛物线上的动点,延长PE、PF分别交直线y=-2于M、N两点,MN交y轴于Q点,求QM·QN的值。
图1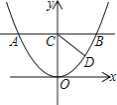 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
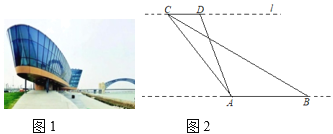
【题目】全国第二届青年运动会是山西省历史上第一次举办的大型综合性运动会,太原作为主赛区,新建了很多场馆,其中在汾河东岸落成了太原水上运动中心,它的终点塔及媒体中心是一个以“大帆船”造型(如图1),外观极具创新,这里主要承办赛艇、皮划艇、龙舟等项目的比赛.“青春”数学兴趣小组为了测量“大帆船”AB的长度,他们站在汾河西岸,在与AB平行的直线l上取了两个点C、D,测得CD=40m,∠CDA=120°,∠ACB=18.5°,∠BCD=26.5°,如图2.请根据测量结果计算“大帆船”AB的长度.(结果精确到0.1m,参考数据:sin26.5°≈0.45,tan26.5°≈0.50,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】传说古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数,比如,他们研究过1,3,6,10,……,由于这些数可以用图中所示的三角形点阵标表示,他们就将其称为三角形数,第n个三角形数可以用![]() 表示.
表示.
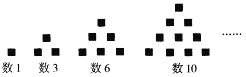
请根据以上材料,证明以下结论:
(1)任意一个三角形数乘8再加1是一个完全平方数;
(2)连续两个三角形数的和是一个完全平方数.
查看答案和解析>>
科目:初中数学 来源: 题型:
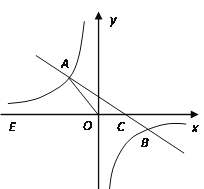
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com