
【题目】抗击疫情,人人有责,某校成立教师志愿者分队,共分宣传、测温、清理(主要厨余垃圾清理)、统计(师生疫情信息统计)四组,为了解教师对这四个小组的参与意愿情况调查,对教师进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表.
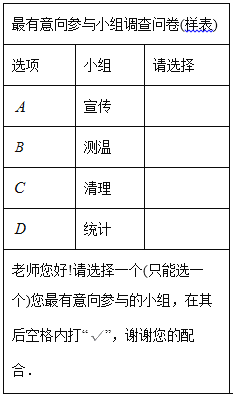
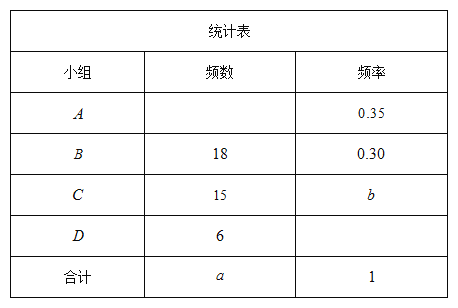
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() _ ,b=_ ;
_ ,b=_ ;
(2)根据调查结果,请你估计该市![]() 名教师中最有意向参与清理小组的人数;
名教师中最有意向参与清理小组的人数;
(3)王老师和李老师选择参与小组,若他们每人从![]() 四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
四个小组中随机选取一个,请用画树状图或列表格的方法,求两人恰好选中同一个的概率.
科目:初中数学 来源: 题型:
【题目】如图①,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移
先向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
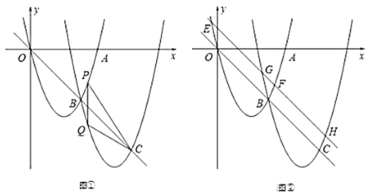
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() (含端点)间的一点,作
(含端点)间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连按
,连按![]() ,
,![]() .当
.当![]() 的面积为
的面积为![]() 时, 求点
时, 求点![]() 的坐标;
的坐标;
(3)如图②,将直线![]() 向上平移,交抛物线
向上平移,交抛物线![]() 于点
于点![]() 、
、![]() ,交抛物线
,交抛物线![]() 于点
于点![]() 、
、![]() ,试判断
,试判断![]() 的值是否为定值,并说明理由.
的值是否为定值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() .
.
(1)求![]() 和
和![]() (用
(用![]() 的代数式表示);
的代数式表示);
(2)若在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最大值为1,求
的最大值为1,求![]() 的值;
的值;
(3)已知点![]() 和点
和点![]() .若二次函数
.若二次函数![]() 的图象与线段
的图象与线段![]() 有两个不同的交点,直接写出
有两个不同的交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() :
:![]() 和二次函数
和二次函数![]() :
:![]()
![]() 图象的顶点分别为
图象的顶点分别为![]() 、
、![]() ,与
,与![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边)和
的左边)和![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),
的左边),
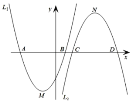
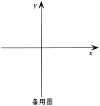
(1)函数![]() 的顶点坐标为______;当二次函数
的顶点坐标为______;当二次函数![]() ,
,![]() 的
的![]() 值同时随着
值同时随着![]() 的增大而增大时,则
的增大而增大时,则![]() 的取值范围是_______;
的取值范围是_______;
(2)判断四边形![]() 的形状(直接写出,不必证明);
的形状(直接写出,不必证明);
(3)抛物线![]() ,
,![]() 均会分别经过某些定点;
均会分别经过某些定点;
①求所有定点的坐标;
②若抛物线![]() 位置固定不变,通过平移抛物线
位置固定不变,通过平移抛物线![]() 的位置使这些定点组成的图形为菱形,则抛物线
的位置使这些定点组成的图形为菱形,则抛物线![]() 应平移的距离是多少?
应平移的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
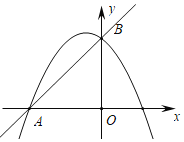
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() 、
、![]() .
.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
(3)如图,当![]() 时,在抛物线上是否存在点
时,在抛物线上是否存在点![]() ,使
,使![]() 的面积为1?若存在,请求出符合条件的所有点
的面积为1?若存在,请求出符合条件的所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 坐标为
坐标为![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]()
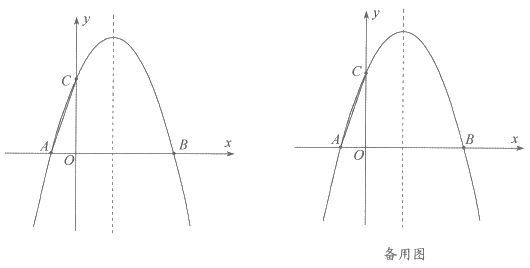
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴右侧抛物线图像上的一动点,设点
轴右侧抛物线图像上的一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①是否存在这样的点![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
②若该动点![]() 在第一象限内,连接
在第一象限内,连接![]() ,当
,当![]() 时,求
时,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
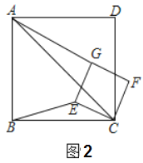
【题目】如图(1),已知点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 垂足为点
垂足为点![]() ,垂足为点
,垂足为点![]() .
.
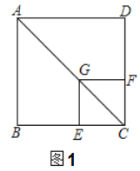
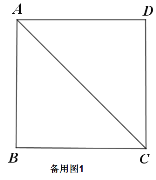
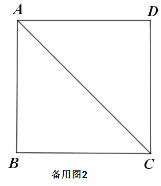
(1)证明与推断:
![]() 求证:四边形
求证:四边形![]() 是正方形;
是正方形;
![]() 推断:
推断:![]() 的值为_ _;
的值为_ _;
(2)探究与证明:
将正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角
角![]() ,如图(2)所示,试探究线段
,如图(2)所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)拓展与运用:
若![]() ,正方形
,正方形![]() 在绕点
在绕点![]() 旋转过程中,当
旋转过程中,当![]() 三点在一条直线上时,则
三点在一条直线上时,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
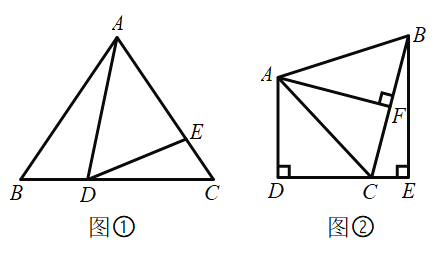
【题目】如图①,在![]() 中,
中,![]() ,点
,点![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的点,且
上的点,且![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如图②,![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“青山绿水”行动中,某社区计划对面积为![]() 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为
的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天各能完成多少面积的绿化;
(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com