

分析 (1)作AH垂直于BC,垂足为H,如图1所示,由∠B=∠BCD=45°,得到三角形ABH为等腰直角三角形,由等腰梯形的两底之差的一半求出BH的长,即为AH的长,由BC-BH求出HC的长,利用勾股定理求出AC的长,由AD与BC平行,得到一对内错角相等,再由已知角相等,利用两角相等的三角形相似得到三角形ADP与三角形CAB相似,由相似得比例求出AP的长即可;
(2)由AD与BC平行,得到一对内错角相等,再由已知角相等,利用两角相等的三角形相似得到三角形ADP与三角形CAB相似,由相似得比例列出y与x的函数解析式,并求出定义域即可;
(3)分两种情况考虑:当点G在线段CD上时,作DM∥EP交AC于点M,如图2所示,同理求出AM的长,进而求出MC的长,由CD-DG求出GC的长,根据GP与MD平行,由平行得比例求出PM的长,由DM与EP平行,根据平行得比例,求出DE的长,根据AD+DE求出AE的长;②当点G在CD的延长线上时,如图3所示,同理求出DE的长,由AD-DE求出AE的长即可.
解答 解:(1)作AH⊥BC于点H,如图1所示: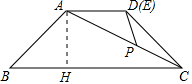
∵∠B=∠BCD=45°,AD=3,BC=9,等腰梯形ABCD,AD=3,BC=9,
∴BH=AH=$\frac{1}{2}$(BC-AD)=$\frac{1}{2}$×(9-3)=3,
∴BH=AH=3,
根据勾股定理得:AB=$\sqrt{A{H}^{2}+B{H}^{2}}$=3$\sqrt{2}$,CH=BC-BH=9-3=6,
∴AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=3$\sqrt{5}$,
∵AD∥BC,
∴∠DAP=∠ACB,
又∠APE=∠B,
∴△ADP∽△CAB,
∴$\frac{AD}{AC}$=$\frac{AP}{BC}$,即$\frac{3}{3\sqrt{5}}$=$\frac{AP}{9}$,
∴AP=$\frac{9\sqrt{5}}{5}$;
(2)如图2所示,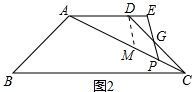
∵AD∥BC,
∴∠DAP=∠ACB,
∵∠APE=∠B,
∴△APE∽△CBA,
∴$\frac{AE}{AC}$=$\frac{AP}{BC}$,即$\frac{3+y}{3\sqrt{5}}$=$\frac{x}{9}$,
∴y=$\frac{\sqrt{5}}{3}$x-3($\frac{9\sqrt{5}}{5}$<x≤3$\sqrt{5}$);
(3)分两种情况考虑:
①当点G在线段CD上时,作DM∥EP交AC于点M,如图2所示,
由(1),同理可得AM=$\frac{9\sqrt{5}}{5}$,
∴CM=$\frac{6\sqrt{5}}{5}$,
∵DG=$\sqrt{2}$,CD=AB=3$\sqrt{2}$,
∴CG=2$\sqrt{2}$,
∵GP∥DM,
∴$\frac{CG}{DG}$=$\frac{CP}{MP}$,即$\frac{2\sqrt{2}}{\sqrt{2}}$=$\frac{\frac{6\sqrt{5}}{5}-MP}{MP}$,
∴MP=$\frac{2\sqrt{5}}{5}$,
∵DM∥EP,
∴$\frac{AD}{DE}$=$\frac{AM}{MP}$,即$\frac{3}{DE}$=$\frac{\frac{9\sqrt{5}}{5}}{\frac{2\sqrt{5}}{5}}$,
解得:DE=$\frac{2}{3}$,
∴AE=AD+DE=3+$\frac{2}{3}$=$\frac{11}{3}$;
②当点G在CD的延长线上时,如图3所示,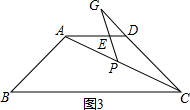
同①可得DE=$\frac{2}{3}$,
∴AE=AD-DE=3-$\frac{2}{3}$=$\frac{7}{3}$.
点评 此题属于相似形综合题,涉及的知识有:平行线等分线段成比例,等腰梯形的性质,等腰直角三角形的判定与性质,勾股定理,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0不是单项式 | B. | $\frac{1}{x}$是单项式 | C. | πx2y的次数是4 | D. | x-$\frac{3}{2}$是整式 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π)
如图,以AB为直径的⊙O与弦CD相交于点E,若AC=2$\sqrt{3}$,AE=3,CE=$\sqrt{3}$,求弧BD的长度.(保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.
等边△ABC高为7$\sqrt{3}$,边长为14.BD为AC边上高,P是BD上的动点,且E是BC上-点,BE=CE,则△PEC的周长最小值为7$\sqrt{3}$+7.查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:判断题
某产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点在原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额-生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,今年最多可获得多少万元的毛利润?
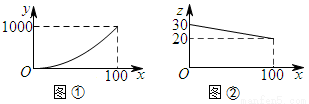
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com