
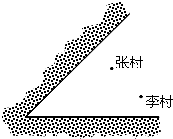
 近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)
近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
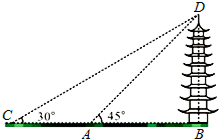 如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).
如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
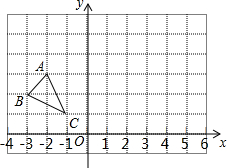 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
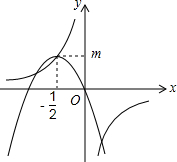 如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )
如图,双曲线y=$\frac{k}{x}$经过抛物线y=ax2+bx的顶点(-$\frac{1}{2}$,m)(m>0),则有( )| A. | a=b+2k | B. | a=b-2k | C. | k<b<0 | D. | a<k<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com