
 如图,线段EF的长为4,O是EF的中点,以OF为边长做正方形OABC,连接AE、CF交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°止,则点P运动的路径长为( )
如图,线段EF的长为4,O是EF的中点,以OF为边长做正方形OABC,连接AE、CF交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°止,则点P运动的路径长为( )| A. | $\frac{\sqrt{2}}{2}$π | B. | $\sqrt{2}$π | C. | 2π | D. | 2$\sqrt{2}$π |
分析 如图,连接AC.首先证明∠EPF=135°,推出点P在与K为圆心的圆上,点P的运动轨迹是$\widehat{EPF}$,在⊙K上取一点M,连接ME、MF、EK、FK,则∠M=180°-∠EPF=45°,推出∠EKF=2∠M=90°,因为EF=4,所以KE=KF=2$\sqrt{2}$,根据弧长公式计算即可解决问题.
解答 解:如图,连接AC.
∵AOCB是正方形,
∴∠AOC=90°,
∴∠AFC=$\frac{1}{2}$∠AOC=45°,
∵EF是直径,
∴∠EAF=90°,
∴∠APF=∠AFP=45°,
∴∠EPF=135°,
∴点P在与K为圆心的圆上,点P的运动轨迹是$\widehat{EPF}$,
在⊙K上取一点M,连接ME、MF、EK、FK,则∠M=180°-∠EPF=45°,
∴∠EKF=2∠M=90°,
∵EF=4,
∴KE=KF=2$\sqrt{2}$,
∴P运动的路径长=$\frac{90π•2\sqrt{2}}{180}$=$\sqrt{2}$π,
故选B.
点评 本题考查正方形的性质、旋转的性质、轨迹、圆等知识,解题的关键是正确发现轨迹的位置,学会添加辅助线,利用圆的有关性质解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:选择题
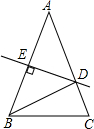 如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )
如图,△ABC中,AB=AC,∠C=72°,AB的垂直平分线DE交AC于D,交AB于E,则∠BDC的度数为( )| A. | 36° | B. | 60° | C. | 72° | D. | 82° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
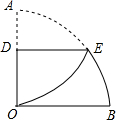 在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.
在扇形纸片AOB中,∠AOB=90°,OA=4,将扇形纸片AOB按如图所示折叠,使对折后点A与点O重合,折痕为DE,则$\widehat{BE}$的长度为$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB2=AC•BC | B. | BC2=AC•BC | C. | AC=$\frac{\sqrt{5}-1}{2}$BC | D. | BC=$\frac{3-\sqrt{5}}{2}$AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=-3或1 | B. | m=1 | C. | m=-3 | D. | m=-3且m≠0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com