
 ��ͼ�٣�������y=ax2+bx+c��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=-x+2����A��C���㣬��AB=2��
��ͼ�٣�������y=ax2+bx+c��x�������ύ��A��B���㣬��y�ύ�ڵ�C��ֱ��y=-x+2����A��C���㣬��AB=2������ ��1�����A��B��C�������꣬���������ߵĽ���ʽ���ⷽ���鼴�ɣ�
��2��������������ͼ���У���DF=2DEʱ����F���꣨4t��2-t��������ͼ2�У���DE=2DFʱ����F���꣨$\frac{5}{2}$t��2-t������취�г����̽�����⣮
��3��������������ͼ�۵�0��t��1ʱ���ص������������EHOGK������ͼ���У���1��t��2ʱ���ص��������ı���OHEA���ֱ���㼴�ɣ�
��� �⣺��1����ֱ��y=-x+2��x�ᡢy��Ľ���ΪA��2��0����C��0��2����AB=2��
��B��4��0����
��A��2��0����B��4��0����C��0��2������y=ax2+bx+c��
��$\left\{\begin{array}{l}{4a+2b+c=0}\\{c=2}\\{16a+4b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2-$\frac{3}{2}$x+2��
��2����OA=OC=2��
���AOC�ǵ���ֱ�������Σ�
��ֱ��l��x�ᣬ
���HEC�ǵ���ֱ�������Σ�
��OA=AB=2��
��HE=DE��
����ͼ���У���DF=2DEʱ����F���꣨4t��2-t����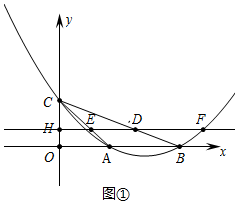
��2-t=$\frac{1}{4}$����4t��2-$\frac{3}{2}$��4t+2��
��t=$\frac{5}{4}$��0����������
����ͼ2�У���DE=2DFʱ����F���꣨$\frac{5}{2}$t��2-t����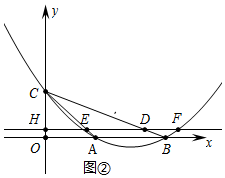
��2-t=$\frac{1}{4}$����$\frac{5}{2}$t��2-$\frac{3}{2}$��$\frac{5}{2}$t+2��
��t=$\frac{44}{25}$��0����������
��������������D���߶�EF�����ȷֵ�ʱ��t��ֵΪ$\frac{5}{4}$s��$\frac{44}{25}$s��
��3������ͼ�۵�0��t��1ʱ���ص������������EHOGK��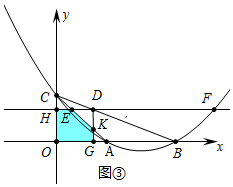
S=S����OHDG-S��DEK=2t•��2-t��-$\frac{1}{2}$t2=-$\frac{5}{2}$t2+4t��
����ͼ���У���1��t��2ʱ���ص��������ı���OHEA��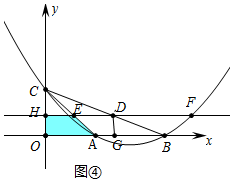
S=$\frac{1}{2}$��t+2����2-t��=-$\frac{1}{2}$t2+2��
����������S=$\left\{\begin{array}{l}{-\frac{5}{2}{t}^{2}+4t}&{��0��t��1��}\\{-\frac{1}{2}{t}^{2}+2}&{��1��t��2��}\end{array}\right.$��
���� ���⿼����κ����ۺ��⡢����ϵ������ƽ���ߵ����ʡ�����ε������֪ʶ������Ĺؼ���ѧ�����Ӧ����ѧ֪ʶ������⣬ѧ���÷������۵�˼��˼�����⣬�����п�ѹ���⣮


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 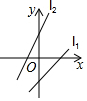 | B�� |  | C�� | 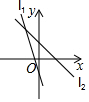 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
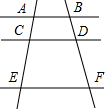 ��ͼ��AB��CD��EF����$\frac{AC}{CE}$=$\frac{1}{2}$����$\frac{BD}{BF}$=$\frac{1}{3}$��
��ͼ��AB��CD��EF����$\frac{AC}{CE}$=$\frac{1}{2}$����$\frac{BD}{BF}$=$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �κ�����������ƽ���� | B�� | ��a��0��x2=a����x��a��һ��ƽ���� | ||
| C�� | 2��ƽ������4 | D�� | ��a��0��x2=a����a��x��һ��ƽ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com