
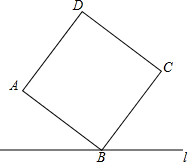
 如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$.
如图,直线l过正方形ABCD的顶点B,点A、C到直线l的距离分别为2和3,则正方形的边长是$\sqrt{13}$. 分析 作AE⊥l于E,CF⊥l于F,如图,AE=2,CF=3,利用正方形的性质得BA=BC,∠ABC=90°,再利用等角的余角相等得∠CBF=∠BAE,则可根据“AAS”判定△ABE≌△BCF,所以AE=BF=2,然后在Rt△BCF中,利用勾股定理计算BC的长即可.
解答 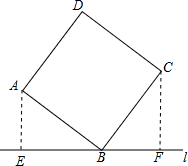 解:作AE⊥l于E,CF⊥l于F,如图,AE=2,CF=3,
解:作AE⊥l于E,CF⊥l于F,如图,AE=2,CF=3,
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴∠ABE+∠CBF=90°,
而∠ABE+∠BAE=90°,
∴∠CBF=∠BAE,
在△ABE和△BCF中
$\left\{\begin{array}{l}{∠AEB=∠BFC}\\{∠BAE=∠CBF}\\{AB=BC}\end{array}\right.$,
∴△ABE≌△BCF,
∴AE=BF=2,
在Rt△BCF中,BC=$\sqrt{B{F}^{2}+C{F}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
即正方形的边长为$\sqrt{13}$.
故答案为$\sqrt{13}$.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了正方形的性质和勾股定理.本题的关键的作辅助线构造两个全等的三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
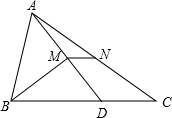 如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN=$\frac{3}{2}$.
如图,在△ABC中,点D在BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若AB=5,BC=8,则MN=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
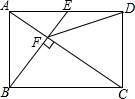 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>-4 | B. | m<$\frac{3}{2}$ | C. | m<-4 | D. | -4<m<$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com