
 如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④.
如图,△ABD,△BCE均为等边三角形,A,B,C三点在同一直线上,点F在AB上,且∠DFE=60°,以下结论:①DF=EF;②AF=BC;③$\frac{FB}{BC}$=$\frac{BE}{DF}$;④DF2=DB•DG,正确的有(填序号)①②④. 分析 可证明△ADF≌△BDE≌△CFE,得出DF=EF=DE,AF=BC=BE;证明△DFG∽△DBF,得到DF2=DB•DG,可知①②④正确.
解答 解:∵△ABD、△BCE均为等边三角形,
∴AB=BD=AD,BC=CE=BE,∠ABD=∠CBE=60°,
∴∠DBE=∠DFE=60°,
∴B、E、D、F四点共圆,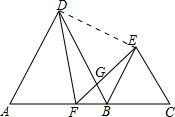
∴∠BDE=∠CFE,
又∵∠CFE+∠AFD=180°-60°=120°=∠ABF+∠AFD,
∴∠BDE=∠CFE=∠ADF,
在△ADF和△BDE中
$\left\{\begin{array}{l}{∠ADF=∠BDE}\\{AD=BD}\\{∠DAF=∠DBE}\end{array}\right.$
∴△ADF≌△BDE
∴AF=BE=BC=CE,
∴AD=AB=FC,
在△ADF和△CFE中,
$\left\{\begin{array}{l}{AD=CF}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$
∴△ADF≌△CFE,
∴DF=EF=DE,AF=BC=BE;
故①②都正确;
∵∠DFE=∠DBF=60°,∠BDF=∠BDF,
∴△DFG∽△DBF,
∴DF2=DB•DG,
故④正确;
故答案为:①②④.
点评 本题主要考查了全等三角形的判定与性质、四点共圆的判定与性质、相似三角形的判定与性质,发现图形中的全等三角形和相似三角形是解决问题的关键.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:填空题
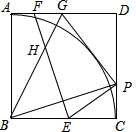 点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)
点P是正方形ABCD的边CD上一点,EF垂直平分BP分别交BC,AD于点E,F,GP⊥EP交AD于G,连接BG交EF于H,有下列结论:①BP=EF;②以BA为半径的⊙B与GP相切;③∠FHG=45°;④若G为AD的中点,则DP=2CP.其中正确的结论是①②③④.(填所有正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2y)(x-8y) | B. | (x+y)(x-16y) | C. | (-4y+x)(4y+x) | D. | (-x-4y)(x+4y) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{8}$ | B. | ±3$\sqrt{8}$ | C. | 6$\sqrt{2}$ | D. | ±3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com