
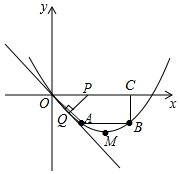
 已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.
已知,如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C,A(1,-1),B(3,-1),动点P从点O出发,沿着x轴正方向以每秒2个单位长度的速度移动,过点P作PQ垂直于直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2),△OPQ与四边形OABC重叠部分的面积为S.分析 (1)设抛物线解析式为y=ax2+bx(a≠0),然后把点A、B的坐标代入求出a、b的值,即可得解,再把函数解析式整理成顶点式形式,然后写出顶点M的坐标;
(2)根据点P的速度求出OP,即可得到点P的坐标,再根据点A的坐标求出∠AOC=45°,然后判断出△POQ是等腰直角三角形,根据等腰直角三角形的性质求出点Q的坐标即可;
(3)求出点Q与点A重合时的t=1,点P与点C重合时的t=1.5,t=2时PQ经过点B,然后分①0<t≤1时,重叠部分的面积等于△POQ的面积,②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积分别列式整理即可得解.
解答 解:(1)设抛物线解析式为y=ax2+bx(a≠0),
把点A(1,-1),B(3,-1)代入得,
$\left\{\begin{array}{l}{a+b=-1}\\{9a+3b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{3}}\\{b=-\frac{4}{3}}\end{array}\right.$,
故抛物线解析式为y=$\frac{1}{3}$x2-$\frac{4}{3}$x;
(2)∵点P从点O出发速度是每秒2个单位长度,
∴OP=2t,
∴点P的坐标为(2t,0),
∵A(1,-1),
∴∠AOC=45°,
∴点Q到x轴、y轴的距离都是$\frac{1}{2}$OP=$\frac{1}{2}$×2t=t,
∴点Q的坐标为(t,-t);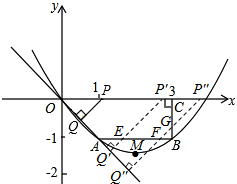
(3)如图,点Q与点A重合时,OP=1×2=2,t=2÷2=1,
点P与点C重合时,OP=3,t=3÷2=1.5,
t=2时,OP=2×2=4,PC=4-3=1,此时PQ经过点B,
所以,分三种情况讨论:
①0<t≤1时,重叠部分的面积等于△POQ的面积,S=$\frac{1}{2}$×(2t)×$\frac{2t}{2}$=t2,
②1<t≤1.5时,重叠部分的面积等于两个等腰直角三角形的面积的差,
S=S△OP′Q′-S△AEQ′=$\frac{1}{2}$×(2t)×$\frac{2t}{2}$-$\frac{1}{2}$×($\sqrt{2}$t-$\sqrt{2}$)2=2t-1;
③1.5<t<2时,重叠部分的面积等于梯形的面积减去一个等腰直角三角形的面积
S=S梯形OABC-S△BGF=$\frac{1}{2}$×(2+3)×1-$\frac{1}{2}$×[1-(2t-3)]2=-2(t-2)2+$\frac{5}{2}$;
所以,S与t的关系式为S=$\left\{\begin{array}{l}{{t}^{2}(0<t≤1)}\\{2t-1(1<t≤1.5)}\\{-2(t-2)^{2}+\frac{5}{2}(1.5<t<2)}\end{array}\right.$.
点评 此题主要考查了二次函数综合题型,主要利用了待定系数法求二次函数解析式,等腰直角三角形的性质,二次函数图象上点的坐标特征,三角形的面积,难点在于(3)随着运动时间的变化,根据重叠部分的形状的不同分情况讨论,作出图形更形象直观.


科目:初中数学 来源: 题型:选择题
| A. | 一个数(不为0)与它的倒数之积是1 | |
| B. | 一个数与它的相反数之和为0 | |
| C. | 两个数的商为-1,这两个数互为相反数 | |
| D. | 两个数的积为1,这两个数互为相反数 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P=20V | B. | P=5V | C. | PV=20 | D. | PV=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
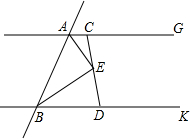 如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.
如图,直线AG∥BK,AE、BE分别平分∠GAB、∠KBA,过点E的直线分别交直线AG、BK于C、D点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | BD | B. | OD | C. | AD | D. | CD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.
如图,在平面直角坐标系xOy中,已知点A(-1,0),点B(0,2),点C(3,0),直线a为过点D(0,-1)且平行于x轴的直线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com