
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() 、
、![]() 上任意点.以线段
上任意点.以线段![]() 为边,在
为边,在![]() 上方作等边
上方作等边![]() ,取边
,取边![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() 的最小值是_______.
的最小值是_______.

【答案】![]()
【解析】
先证明点F、B、E、H四点共圆,进而可得∠FBH=∠FEH=60°,再根据![]() ,
,![]() 求得tan∠ABD=
求得tan∠ABD=![]() ,进而可得∠ABD=60°,由此可得点B、H、D在同一直线上,则当CH⊥BD时,CH取得最小值,最后根据等积法求得CH的最小值即可.
,进而可得∠ABD=60°,由此可得点B、H、D在同一直线上,则当CH⊥BD时,CH取得最小值,最后根据等积法求得CH的最小值即可.
解:如图,连接FH,BH,BD,
∵在矩形ABCD中,
∴∠FBE=∠A=∠BCD=90°,![]() ,
,![]() ,
,
∴在Rt△BCD中,![]() ,
,
∵在等边![]() 中,点H为EG的中点,
中,点H为EG的中点,
∴FH⊥GE,∠FEH=60°,
∴∠FHE=90°,
又∵∠FBE=90°,
∴点F、B、E、H四点共圆,
∴∠FBH=∠FEH=60°,
∵在Rt△ABD中,![]() ,
,![]() ,
,
∴tan∠ABD=![]() ,
,
∴∠ABD=60°,
∴点B、H、D在同一直线上,
∴当CH⊥BD时,CH取得最小值,
若CH⊥BD,则![]()
∴![]() ,
,
∴CH的最小值为![]() ,
,
故答案为:![]()



科目:初中数学 来源: 题型:
【题目】教育未来指数是为了评估教育系统在培养学生如何应对快速多变的未来社会方面所呈现的效果.现对教育未来指数得分前35名的国家和地区的有关数据进行收集、整理、描述和分析后,给出了部分信息.
a.教育未来指数得分的频数分布直方图(数据分成7组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
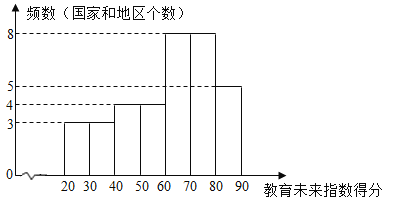
b.教育未来指数得分在![]() 这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
这一组的是:61.2 62.8 64.6 65.2 67.2 67.3 67.5 68.5
c.35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图如下:
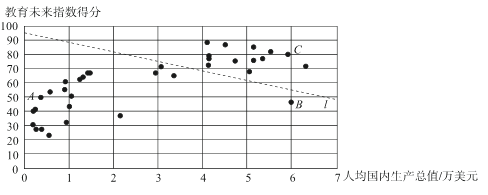
d.中国和中国香港的教育未来指数得分分别为32.9和68.5.
(以上数据来源于《国际统计年鉴(2018)》和国际在线网)
根据以上信息,回答下列问题:
(1)中国香港的教育未来指数得分排名世界第______;
(2)在35个国家和地区的人均国内生产总值和教育未来指数得分情况统计图中,包括中国香港在内的少数几个国家和地区所对应的点位于虚线l的上方,请在图中用“○”画出代表中国香港的点;
(3)在教育未来指数得分比中国高的国家和地区中,人均国内生产总值的最大值约为_____万美元;(结果保留一位小数)
(4)下列推断合理的是__________.(只填序号即可)
①相较于点![]() 所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
所代表的国家和地区,中国的教育未来指数得分还有一定差距,“十三五”规划提出“教育优先发展,教育强则国家强”的任务,进一步提高国家教育水平;
②相较于点![]() 所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
所代表的国家和地区,中国的人均国内生产总值还有一定差距,中国提出“决胜全面建成小康社会”的奋斗目标,进一步提高人均国内生产总值.
查看答案和解析>>
科目:初中数学 来源: 题型:
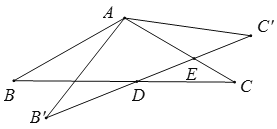
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.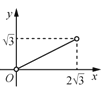 B.
B.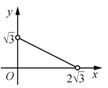 C.
C.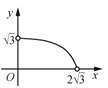 D.
D.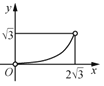
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点![]() 在平面直角坐标系
在平面直角坐标系![]() 中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点
中,按图中箭头所示方向运动,第1次从原点运动到点(1,2),第2次接着运动到点(2,0),第3次接着运动到点(3,1),第4次接着运动到点(4,0),……,按这样的运动规律,经过第27次运动后,动点![]() 的坐标是( )
的坐标是( )
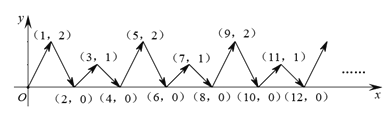
A.(26,0)B.(26,1)C.(27,1)D.(27,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)求点![]() 坐标;
坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 及抛物线在
及抛物线在![]() 两点之间的部分围成的封闭区域(不含边界)记为
两点之间的部分围成的封闭区域(不含边界)记为![]() .
.
①当![]() 时,结合函数图象,直接写出区域
时,结合函数图象,直接写出区域![]() 内的整点个数;
内的整点个数;
②如果区域![]() 内有2个整点,请求出
内有2个整点,请求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,六边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
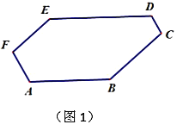
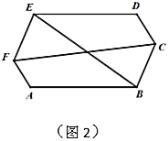
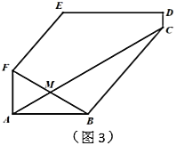
(1)找出这个六边形中所有相等的内角_______.证明其中的一个结论.
(2)如果![]() ,证明对角线
,证明对角线![]() ,
,![]() 互相平分;
互相平分;
(3)如图,如果![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分对角线
平分对角线![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
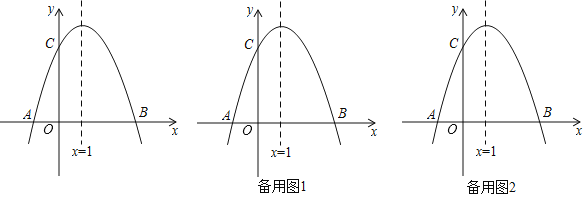
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com