
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为
的顶点为![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() (点
(点![]() 在点
在点![]() 的左侧).
的左侧).

(1)求点![]() 坐标;
坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 及抛物线在
及抛物线在![]() 两点之间的部分围成的封闭区域(不含边界)记为
两点之间的部分围成的封闭区域(不含边界)记为![]() .
.
①当![]() 时,结合函数图象,直接写出区域
时,结合函数图象,直接写出区域![]() 内的整点个数;
内的整点个数;
②如果区域![]() 内有2个整点,请求出
内有2个整点,请求出![]() 的取值范围.
的取值范围.
【答案】(1)A(a,0);(2)①4;②![]()
【解析】
(1)根据抛物线顶点坐标求法求解即可;
(2)①画出图像,根据图像以及整点的概念求解即可;
②由①推出a<0,分别求出有2个整点和3个整点时a的取值,再得出取值范围.
解:(1)∵抛物线的解析式为:![]() ,
,
∴可得顶点坐标为:A(a,0);
(2)①∵a=0,
∴抛物线表达式为:![]() ,
,
令![]() ,
,
解得:x1=![]() ,x2=
,x2=![]() ,
,
∵![]() ,
,![]() ,
,
∴区域![]() 内的整点有(0,1),(0,2),(1,2),(1,3)共4个整点;
内的整点有(0,1),(0,2),(1,2),(1,3)共4个整点;
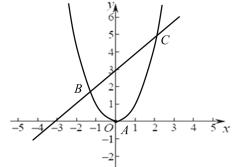
②由①可知当a=0时有4个整点,
当a>0时,对称轴在y轴右侧,此时有更多整点,
∴a<0,
∵抛物线的解析式为:![]() ,
,
∴抛物线的顶点在x轴,开口向上,
当抛物线在直线y=x+3左侧且两者相切时,没有整点,
当抛物线向右平移时,第一个整点为(-1,1),代入抛物线,
![]() ,
,
解得:a=-2或0(舍),
第二个整点为(0,2),代入抛物线,
![]() ,
,
解得:a=![]() (舍)或
(舍)或![]() ,
,
第三个整点为(0,1),代入抛物线,
![]() ,
,
解得:a=1(舍)或-1,
综上:a的取值范围是:![]() .
.


科目:初中数学 来源: 题型:
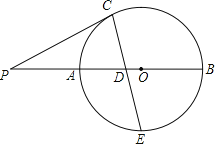
【题目】如图,AB为⊙O的直径,P为BA延长线上一点,点C在⊙O上,连接PC,D为半径OA上一点,PD=PC,连接CD并延长交⊙O于点E,且E是![]() 的中点.
的中点.
(1)求证:PC是⊙O的切线;
(2)求证:CDDE=2ODPD;
(3)若AB=8,CDDE=15,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售10台A型和20台B型加湿器的利润为2500元,销售20台A型和10台B型加湿器的利润为2000元
(1)求每台A型加湿器和B型加湿器的销售利润;
(2)该商店计划一次购进两种型号的加湿器共100台,其中B型加湿器的进货量不超过A型加湿器的2倍,设购进A型加湿器x台.这100台加湿器的销售总利润为y元
①求y关于x的函数关系式;
②该商店应怎样进货才能使销售总利润最大?
(3)实际进货时,厂家对A型加湿器出厂价下调m(0<m<100)元,且限定商店最多购进A型加湿器70台,若商店保持两种加湿器的售价不变,请你根据以上信息及(2)中条件,设计出使这100台加湿器销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一大、一小两个等腰直角三角形拼在一起,![]() ,连接
,连接![]() .
.
(1)如图1,若![]() 三点在同一条直线上,则
三点在同一条直线上,则![]() 与
与![]() 的关系是 ;
的关系是 ;
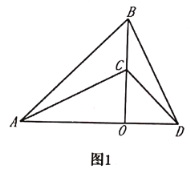
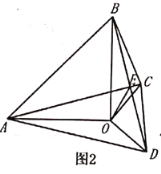
(2)如图2,若![]() 三点不在同一条直线上,
三点不在同一条直线上,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,猜想
,猜想![]() 之间的数量关系,并给予证明;
之间的数量关系,并给予证明;
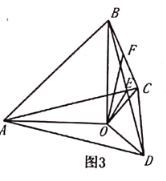
(3)如图3,在(2)的条件下作![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 与
与![]() 之间的关系.
之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过直线外一点作已知直线的平行线“的尺规作图过程.

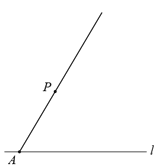
已知:如图,直线![]() 和直线
和直线![]() 外一点
外一点![]() .
.
求作:直线![]() ,使直线
,使直线![]() 直线
直线![]() .
.
作法:如图,
①在直线![]() 上任取一点
上任取一点![]() ,作射线
,作射线![]() ;
;
②以![]() 为圆心,
为圆心,![]() 为半径作弧,交直线
为半径作弧,交直线![]() 于点
于点![]() ,连接
,连接![]() ;
;
③以![]() 为圆心,
为圆心,![]() 长为半径作弧,交射线
长为半径作弧,交射线![]() 于点
于点![]() ;分别以
;分别以![]() 为圆心,大于
为圆心,大于![]() 长为半径作弧,在
长为半径作弧,在![]() 的右侧两弧交于点
的右侧两弧交于点![]() ;
;
④作直线![]() ;
;
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图中的图形;
(2)完成下面的证明:
证明:由作图可知![]() 平分
平分![]() ,
,
![]() .
.
又![]() ,
,
![]() .(_______________________________)(填依据1).
.(_______________________________)(填依据1).
![]() ,
,
![]() .
.
![]() ,∴直线
,∴直线![]() 直线
直线![]() .(______________________)(填依据2).
.(______________________)(填依据2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了解初中学生参加综合实践活动的情况,随机抽取了本市初一、初二、初三年级各![]() 名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.
名学生进行了调查,调查结果如图所示,请你根据图中的信息回答问题.

(1)在被调查的学生中,参加综合实践活动的有多少人,参加科技活动的有多少人;
(2)如果本市有![]() 万名初中学生,请你估计参加科技活动的学生约有多少名.
万名初中学生,请你估计参加科技活动的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)“校园诗歌大赛”结束后,张老师和李老师将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图部分信息如下:
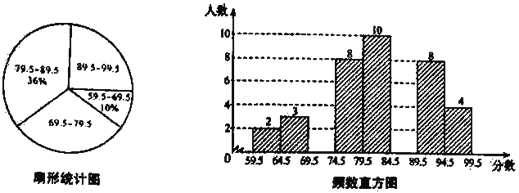
(1)本次比赛参赛选手共有 人,扇形统计图中“69.5~79.5”这一组人数占总参赛人数的百分比为 ;
(2)赛前规定,成绩由高到低前60%的参赛选手获奖.某参赛选手的比赛成绩为78分,试判断他能否获奖,并说明理由;
(3)成绩前四名是2名男生和2名女生,若从他们中任选2人作为获奖代表发言,试求恰好选中1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月“停课不停学”期间,某校采用简单随机抽样的方式调查本校学生参加第一天线上学习的时长,将收集到的数据制成不完整的频数分布表和扇形图,如下所示:
组别 | 学习时长(分钟) | 频数(人) |
第1组 | x≤40 | 3 |
第2组 | 40<x≤60 | 6 |
第3组 | 60<x≤80 | m |
第4组 | 80<x≤100 | 18 |
第5组 | 100<x≤120 | 14 |

(1)求m,n的值;
(2)学校有学生2400人,学校决定安排老师给““线上学习时长”在x≤60分钟范围内的学生打电话了解情况,请你根据样本估计学校学生“线上学习时长”在x≤60分钟范围内的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com