
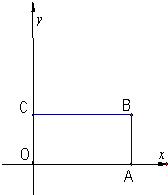
 在平面直角坐标系中,正方形OABC的顶点坐标分别为O(0,0)、A(100,0)、B(100,100)、C(0,100).若正方形OABC内部(边界及顶点除外)一格点P满足:S△POA×S△PBC=S△PAB×S△POC,就称格点P为“好点”,则正方形OABC内部“好点”的个数为( )个.(注:所谓“格点”,是指平面直角坐标系中横、纵坐标均为整点)
在平面直角坐标系中,正方形OABC的顶点坐标分别为O(0,0)、A(100,0)、B(100,100)、C(0,100).若正方形OABC内部(边界及顶点除外)一格点P满足:S△POA×S△PBC=S△PAB×S△POC,就称格点P为“好点”,则正方形OABC内部“好点”的个数为( )个.(注:所谓“格点”,是指平面直角坐标系中横、纵坐标均为整点)

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com