
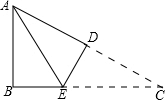
 如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm.
如图,在△ABC中,AB=3cm,BC=7cm,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为10cm. 分析 首先根据翻折变换的性质,可得AE=CE,然后根据三角形的周长的求法,可得△ABE的周长等于AB和BC的长度和,据此解答即可.
解答 解:∵将△ABC折叠,使点C与点A重合,折痕为DE,
∴AE=CE,
∴△ABE的周长=AB+BE+AE
=AB+(BE+CE)
=AB+BC
=3+7
=10(cm),
即△ABE的周长为10cm.
故答案为:10cm.
点评 (1)此题主要考查了翻折变换(折叠问题),要熟练掌握,解答此题的关键是要明确:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
(2)此题还考查了三角形的周长的求法,要熟练掌握,解答此题的关键是判断出:BE+CE=BC.


科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | A | B | C | D |
| 时间t(h) | t<1 | 1≤t<2 | 2≤t<3 | t≥3 |
| 人数 | 5a | 5b | 5c | 5d |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com