
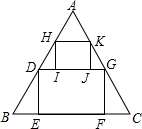 如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.
如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2. 分析 作AQ⊥BC于Q,交HK于M,交DG于N,如图,根据等边三角形的性质得AQ=$\frac{\sqrt{3}}{2}$BC=15$\sqrt{3}$,再由DG∥BC得△ADG∽△ABC,设DE=x,则NQ=x,AN=15$\sqrt{3}$-x,利用相似比可得DG=$\frac{90-2\sqrt{3}x}{3}$,利用矩形面积得x•$\frac{90-2\sqrt{3}x}{3}$=100$\sqrt{3}$,解得x1=10$\sqrt{3}$,x2=5$\sqrt{3}$,然后分类讨论:当x=10$\sqrt{3}$时,DG=10,设HI=a,则MN=a,AM=15$\sqrt{3}$-10$\sqrt{3}$-a=5$\sqrt{3}$-a,通过证明△AHK∽△ADG,利用相似比计算出HK=$\frac{30-2\sqrt{3}a}{3}$,则S长方形HIJK=a•$\frac{30-2\sqrt{3}a}{3}$=-$\frac{2\sqrt{3}}{3}$a2+10a;同理可得当x=5$\sqrt{3}$时,DG=20,S长方形HIJK=-$\frac{2\sqrt{3}}{3}$a2+20a,根据二次函数的最值问题分别求出两种情况下的长方形纸片HIJK的面积的最大值,从而可确定最大的长方形纸片HIJK的面积.
解答 解:作AQ⊥BC于Q,交HK于M,交DG于N,如图,
∵△ABC为等边三角形,
∴AQ=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}}{2}$×30=15$\sqrt{3}$,
∵DG∥BC,
∴△ADG∽△ABC,
∴$\frac{DG}{BC}$=$\frac{AN}{AQ}$,
设DE=x,则NQ=x,AN=15$\sqrt{3}$-x
∴$\frac{DG}{30}$=$\frac{15\sqrt{3}-x}{15\sqrt{3}}$,解得DG=$\frac{90-2\sqrt{3}x}{3}$,
∵DE•DG=100$\sqrt{3}$,即x•$\frac{90-2\sqrt{3}x}{3}$=100$\sqrt{3}$,
整理得x2-15$\sqrt{3}$x+150=0,解得x1=10$\sqrt{3}$,x2=5$\sqrt{3}$,
当x=10$\sqrt{3}$时,DG=10,设HI=a,则MN=a,AM=15$\sqrt{3}$-10$\sqrt{3}$-a=5$\sqrt{3}$-a,
∵HK∥BC,
∴△AHK∽△ADG,
∴$\frac{HK}{DG}$=$\frac{AM}{AN}$,即$\frac{HK}{10}$=$\frac{5\sqrt{3}-a}{5\sqrt{3}}$,解得HK=$\frac{30-2\sqrt{3}a}{3}$,
∴S长方形HIJK=a•$\frac{30-2\sqrt{3}a}{3}$=-$\frac{2\sqrt{3}}{3}$a2+10a=-$\frac{2\sqrt{3}}{3}$(a-$\frac{5\sqrt{3}}{2}$)2+$\frac{25\sqrt{3}}{2}$,
∴a=$\frac{5\sqrt{3}}{2}$时,S长方形HIJK的最大值为$\frac{25\sqrt{3}}{2}$,
当x=5$\sqrt{3}$时,DG=20,设HI=a,则MN=a,AM=15$\sqrt{3}$-5$\sqrt{3}$-a=10$\sqrt{3}$-a,
∵HK∥BC,
∴△AHK∽△ADG,
∴$\frac{HK}{DG}$=$\frac{AM}{AN}$,即$\frac{HK}{20}$=$\frac{10\sqrt{3}-a}{10\sqrt{3}}$,解得HK=$\frac{60-2\sqrt{3}a}{3}$,
∴S长方形HIJK=a•$\frac{60-2\sqrt{3}a}{3}$=-$\frac{2\sqrt{3}}{3}$a2+20a=-$\frac{2\sqrt{3}}{3}$(a-5$\sqrt{3}$)2+50$\sqrt{3}$,
∴a=5$\sqrt{3}$时,S长方形HIJK的最大值为50$\sqrt{3}$,
综上所述,能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.
故答案为50$\sqrt{3}$.
点评 本题考查了相似三角形的应用:通过证明三角形相似,利用相似比表示线段之间的关系或计算线段的长.也考查了二次函数的最值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{{\begin{array}{l}x+y=21\\ 5x=2y\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}x+y=21\\ 2x=5y\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}2x+5y=21\\ 2x=5y\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}2x+5y=21\\ 5x=2y\end{array}}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B. | $3\sqrt{2}-2\sqrt{2}=1$ | C. | $\sqrt{3^2}=3$ | D. | $\sqrt{9}=±3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
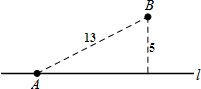 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com