
分析 首先根据题意画出函数图象,分两种情况,但是直线都过(0,3),分别求出A,B点的坐标,再利用待定系数法求出一次函数的解析式.
解答 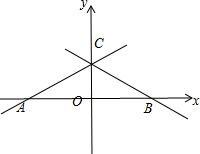 解:①∵一次函数的图象y=kx+b与两坐标轴围成的三角形的面积是6,
解:①∵一次函数的图象y=kx+b与两坐标轴围成的三角形的面积是6,
∴$\frac{1}{2}$OB×CO=6,
$\frac{1}{2}$×OB×3=6,
BO=4,
∴B(4,0)
∵y=kx+b的图象过点(0,3),(4,0),
∴$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$;
②∵一次函数的图象y=kx+b与两坐标轴围成的三角形的面积是6,
∴$\frac{1}{2}$OA×CO=6,
$\frac{1}{2}$×OA×3=6,
AO=4,
∴A(-4,0)
∵y=kx+b的图象过点(0,3),(-4,0),
∴$\left\{\begin{array}{l}{-4k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$,
∴k=±$\frac{3}{4}$
点评 此题主要考查了待定系数法求一次函数解析式,关键是根据题意画出图象,然后再分情况讨论,不要漏掉任何一种情况.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:填空题
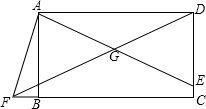 如图,四边形ABCD是矩形,E是CD上一点,连接AE,取AE的中点G,连接DG并延长交CB延长线于点F,连接AF,∠AFC=3∠EAD,若DG=4,BF=1,则AB的长为$\sqrt{15}$.
如图,四边形ABCD是矩形,E是CD上一点,连接AE,取AE的中点G,连接DG并延长交CB延长线于点F,连接AF,∠AFC=3∠EAD,若DG=4,BF=1,则AB的长为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 3 | a | b | c | -1 | 2 | … |
| A. | 3 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
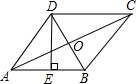 如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )
如图,菱形ABCD的周长为40cm,对角线AC、BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm;②BE=4cm;③BD=4$\sqrt{5}$cm;④AC=8$\sqrt{5}$cm;⑤S菱形ABCD=80cm,正确的有( )| A. | ①②④⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ①②③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
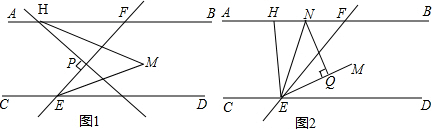
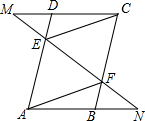 如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.
如图,已知在平行四边形ABCD中,E、F分别是边AD、BC上的点,且DE=BF,过E、F两点作直线,分别与CD、AB的延长线相交于点M、N,连接CE、AF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
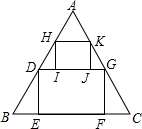 如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.
如图,从边长为30cm的等边△ABC纸片中剪出面积为100$\sqrt{3}$cm2的长方形纸片DEFG,为了更充分的利用剪剩下的纸片△ADG,则能剪出的最大的长方形纸片HIJK的面积为50$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
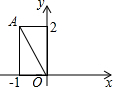 如图,已知点A(-1,2),将线段OA绕O点顺时针方向旋转90°后,得到线段OA′,则点A′的坐标是( )
如图,已知点A(-1,2),将线段OA绕O点顺时针方向旋转90°后,得到线段OA′,则点A′的坐标是( )| A. | (-3,-2) | B. | (2,2) | C. | (3,0) | D. | (2,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com